games101课程笔记13-Ray Tracing

光追，启动！

开始之前：为什么要使用光线追踪？

因为光栅化（rasterization）不能很好地解决全局光照里的一系列问题：

• 软阴影
• 光线弹射不止一次时的情况
  • 磨砂质感（glossy reflection）物体上的环境映射
  • 间接光照计算

Whitted-Style Ray Tracing

前置：对光线的设定

• 光沿直线传播，并且本身就是直线
• 光线没有碰撞现象（即使两条光线交叉时）
• 光线具有可逆性（光路是可逆的）

光线渲染

因为光路是可逆的，所以这里假设光线是由眼睛发出的，并由光源接收（这里假设眼睛和光源都是一个点）

视线（视点出发经过成像平面的一个像素点的射线）可以分为两个部分：primary ray和secondary rays（包含所有经过反射和折射的线路）。

在视线和物体相交后，将交点和光源连线（这条线称为shadow rays）如果这条线段没有被遮挡，则可以认为这一部分是可以照亮的。

然后将所有的颜色叠加起来可以算出这个像素点的颜色。

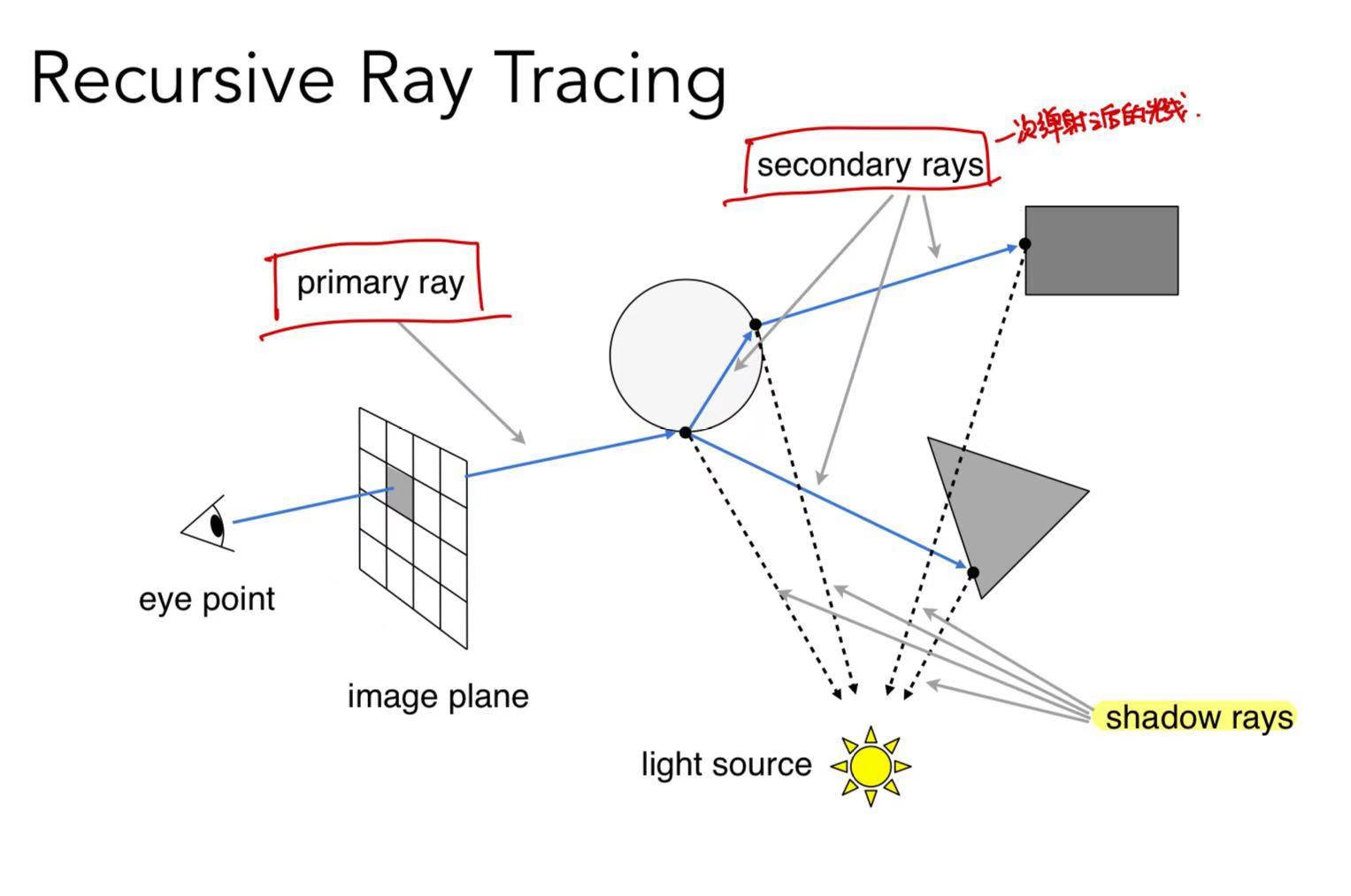
如何计算射线和表面的交点

射线由原点（origin）和方向组成，可以表示为：
$$
r(t)=o+td(0≤t<+∞)
$$
其中，t表示时刻。

光线和隐式表面的交点

隐式表面上的点满足：
$$
P：f(P)=0
$$
联立射线方程，可以解得交点：
$$
f(o+td)=0
$$
你将得到，所有满足实根、正根要求的就是要求的交点。

如何计算射线和网格的交点

一个规律：从平面上的点为原点射出一条射线，如果点在网格内，那么这条射线和网格的交点为奇数个；如果点在网格外，那么这条射线和网格的交点则为偶数个。

简化这个问题：

• 忽略光线和平面平行的情况，此时光线和平面的交点只有0和1两种。

计算射线和三角形的交点

方法一

分为两步：

• 求光线和平面的交点
• 判断这个交点是否在三角形内

平面可以由一个法向量N和平面上的一个点P'表示，平面上的点P可以表示为：
$$
P:(p-p’)·N=0
$$
和之前一样，联立射线方程，可以解得相交时间t。
$$
t=\frac{(p’-o)·N}{d·N}(0≤t<+∞)
$$
方法二 Möller Trumbore Algorithm（MT算法）

另外，还有一种一步到位的方法。射线和平面的交点可以表示为重心坐标的形式，联立可得：
$$
o+td=(1-b_1-b_2)P_o+b_1P_1+b_2P_2(b_1,b_2,1-b_1-b_2,t≥0)
$$
代入三角形顶点的三个维度的坐标，可以获得一个线性方程组（可以使用克拉默法则解出），得到t,b1,b2。

方法三（求交加速方法，使用包围盒（Bounding Volumes））

用简单的形状将物体框起来，在光线和三角面片求交前先确保光线能够碰到包围盒。

包围盒是由三组对面（slab）形成的交集

常使用Axis-Aligned Bounding Box(AABB)这种包围盒，这个包围盒的几个平面与坐标轴平面是平行的。这时，求解射线和平面的交线时只需考虑单个维度的计算即可（因为平面总是和轴平面是平行的），大大减少了计算量。

如何求光线和包围盒的交点呢？

1. 求出光线和三组对面的交点，记录射线和对面交点的进入点和离开点。

2. 然后取这三组交点的交集，满足：
   $$
   t_{enter}=max(t_{min}),t_{exit}=min(t_{max})
   $$

3. 当且仅当满足这个要求时，认为光线是和包围盒相交的：
   $$
   t_{enter}<t_{exit},t_{exit}≥0
   $$

加速结构（承接上文的bounding box）

Uniform grid

将场景划分为网格，通过网格判断光线与物体的相交情况。

构建uniform grids的步骤为：

1. 找到包围盒
2. 创建grid
3. 存储每个对象到格子里

此时，判断光线是否与物体相交的问题转换为先判断光线是否与格子相交，然后判断是否与各自内的物体相交

这里需要考虑grid的分辨率的问题：

• 如果resolution太小，则失去了划分的以意
• 如果resolution太大，则会降低效率

anyway，格子通常只适用于规整的场景，相反，物体位置较为稀疏的场景就不适用这种划分方案，因为此时很多格子都不存储物体，大量时间被浪费在了光线与格子的求交上。

Spatial Partition

通常有Oct-Tree（八叉树） 、KD-Tree 以及 BSP-Tree 三种划分方案

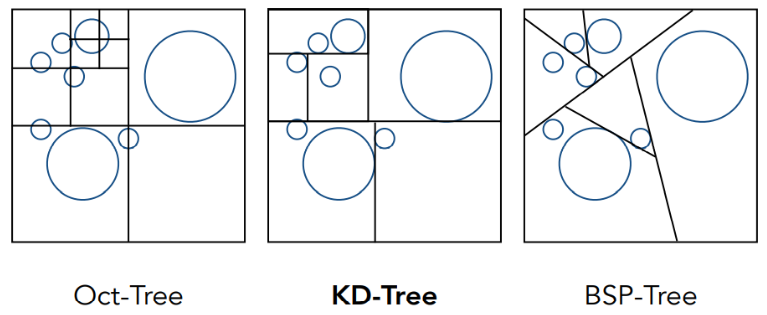
• Oct-Tree：每次迭代都将区域沿着坐标轴切分为均匀八块，按一定规则停止切分（如切分得到的区域中，只有一块含有物体；或此时的区域已经较小）
• KD-Tree：按坐标轴顺序交替切分，每次划分总会在原来的区域上生成新的区域
• BSP-Tree：每次都是沿着一定方向进行切分（非水平或竖直）

最实用的是KD-Tree

Data Structure for KD-Tree

中间节点存储的信息有：

• 沿着划分的轴
• 切分的平面信息
• 子节点的指针

叶子节点存储的信息有：

• 切分区域内的物体列表

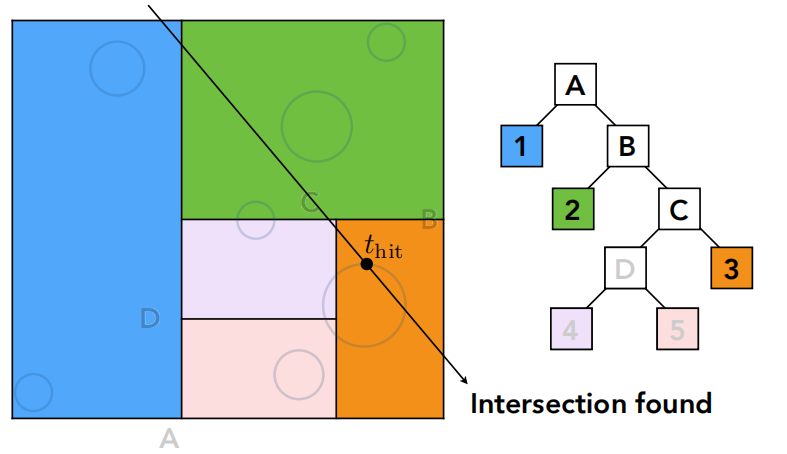
Traversing a KD-Tree

1. 发射光线从根节点出发，分别判断光线与左右节点是否相交，若相交则进入2；否则，则与节点不相交
2. 递归判断相交直至叶子节点，若与叶子节点相交，进入3
3. 挨个判断叶子节点存储物体与光线的相交情况

Problem

• 很难判定三角形是否和包围盒有交集（很难实现）
• 一个物体可能会存储在多个格子里，不够只管

Object Partition & Bounding Volume Hierarchy (BVH)

为了解决KD-Tree的痛点，更换一种划分方法，即在场景中对物体进行划分，此时就不用考虑三角形与包围盒的求交问题

它本质是将一个场景用一个包围盒包住，然后按照一定划分方案将盒子划分成不同的子区域，不同子区域都需要包含三角形，最终划分到叶子节点时，每个叶子节点就包含了一些三角形，即包含了对应的一些物体：

优缺点

• 优点
  • 一个物体只会出现在一个格子里面
  • 格子之间可能会相交（尽可能让重叠的部分小一些）

Building BVHs

划分的三种方法（在格子中物体个数小于一定值时停止）：

1. 按轴的顺序交替划分（KD-Tree）
2. 按最长的边进行划分
3. 在物体三角形数目的最中间对物体进行划分（这里的最中间指的是划分后，两边的三角形数目基本一致）

Data Structure

• 中间节点（Internal nodes）：该节点对应的包围盒和子节点的指针
• 叶子节点（Leaf nodes）：该节点对应的包围盒和包围盒里面的物体列表

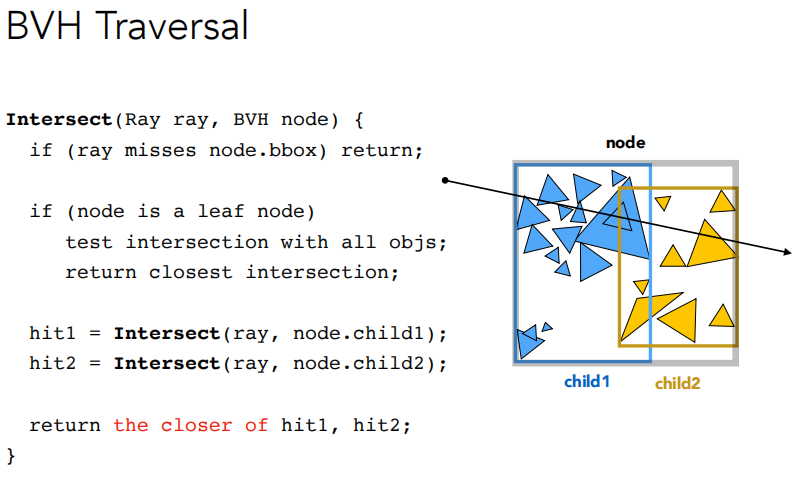
BVH Traversal

使用递归的方法

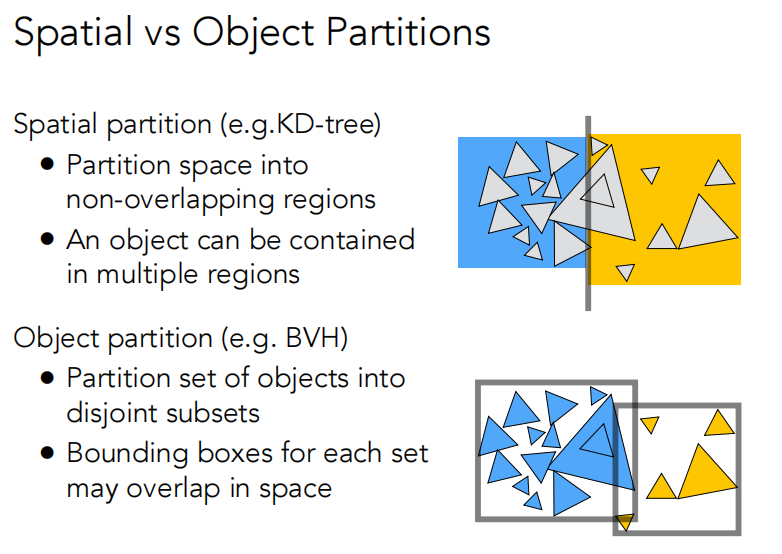
Spatial vs Object Partition

Radiometry