games101课程笔记10-Graphics
现在是,bezier曲线时间。
隐式表达
能够很方便判断点与平面的关系(在平面上/内/外)
经典的隐式表达方法
algebraic surfaces
不直观,而且难以表示复杂的物体
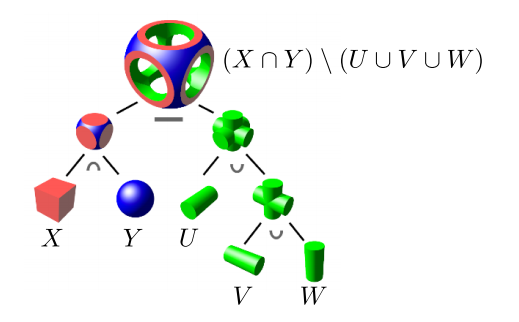
constructive solid geometry(CSG)
通过几何形状间的布尔预算构造图形
signed distance function(SDF)
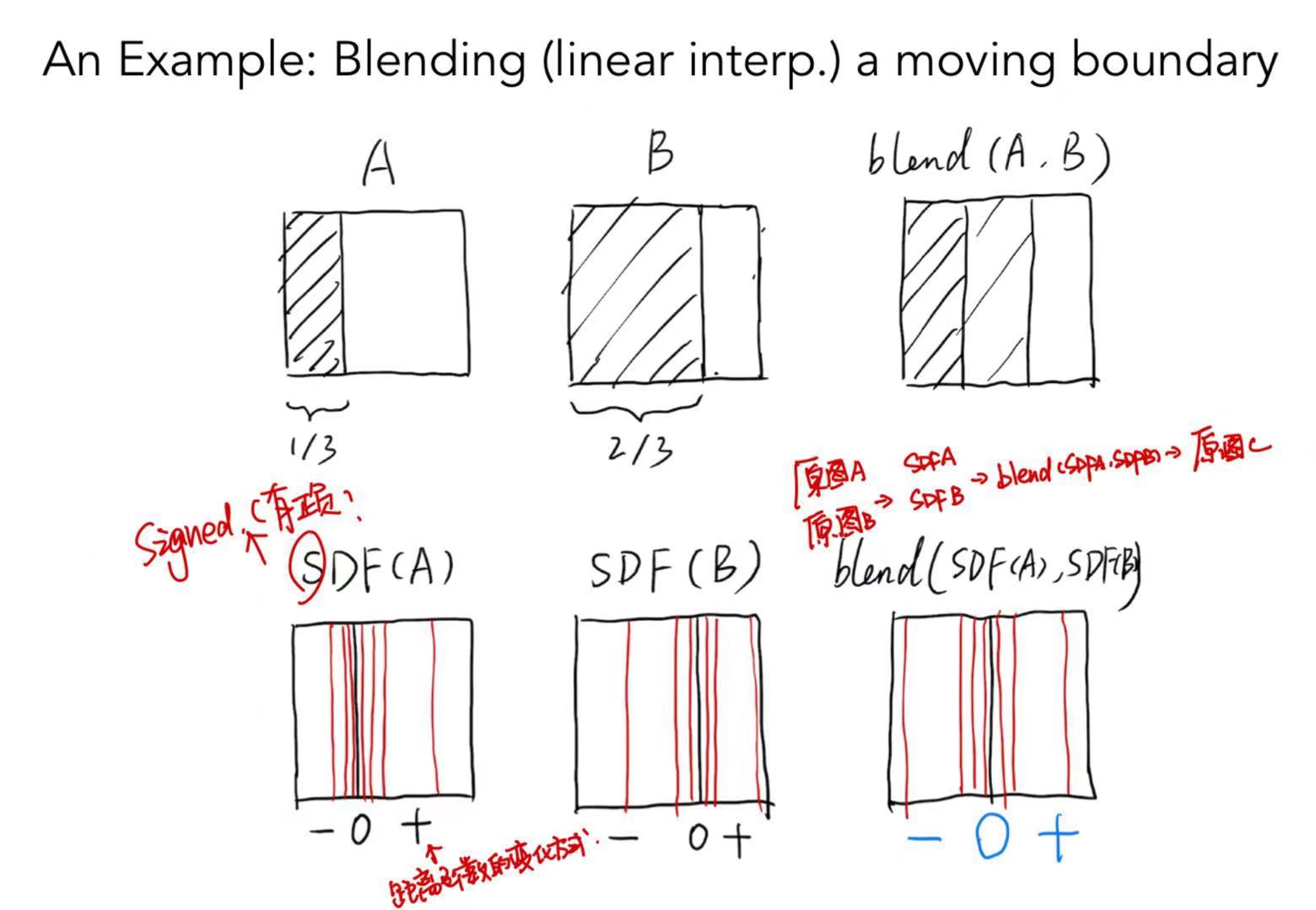
融合距离函数:描述空间上的点到表面的最近距离
举个栗子:在2维场景中,如果直接对A和B进行blend操作,会将原来的表面分为三个层次;
如果先对A和B用SDF表示(变化边界记为0,左右分别为正和负),再进行blend操作后(此时,0的部分在中间位置)再转回原本的表示方法的话,会将原来的表面分为两部分。
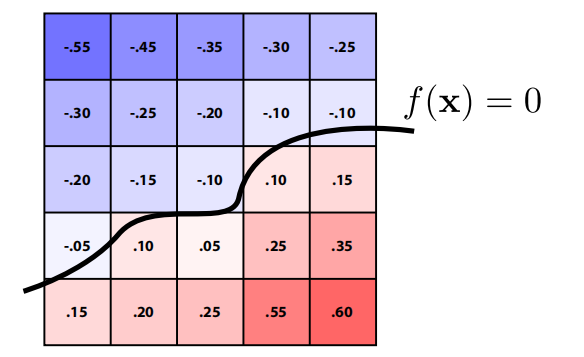
level set methods
用一个表格来存储数据描述物体的方式。距离函数f(x)为0的位置就是物体的表面。
应用于医学中的信息表示(CT,MRI,etc.),以及物理模拟中(模拟水花)
fractals(分形)
常用于描述自然现象。
优缺点
优点:
- 表示容易(例如可以仅使用函数说明)
- 容易查询某些关系(inside object, distance to surface)
- 容易求得射线与平面的交点
- 能够准确的表示一些简单的形状,不存在采样频率不够的问题
- 容易处理拓扑上的变化
缺点:
- 难以表示复杂的形状
显式表达
所有的点通过直接给出或者参数映射的方式给出
采样很方便,能够轻松判断点是否在平面上
经典的显式表达方法
点云
最简单的表达方式(通过点的坐标表示)
能够简单表示任意的几何形状
适用大型的数据集
经常被转换为多边形网格
但是在采样率较低的情况下不太好用
多边形网格
存储顶点&几何形状(通常为三角形和四边形)
几何处理方法
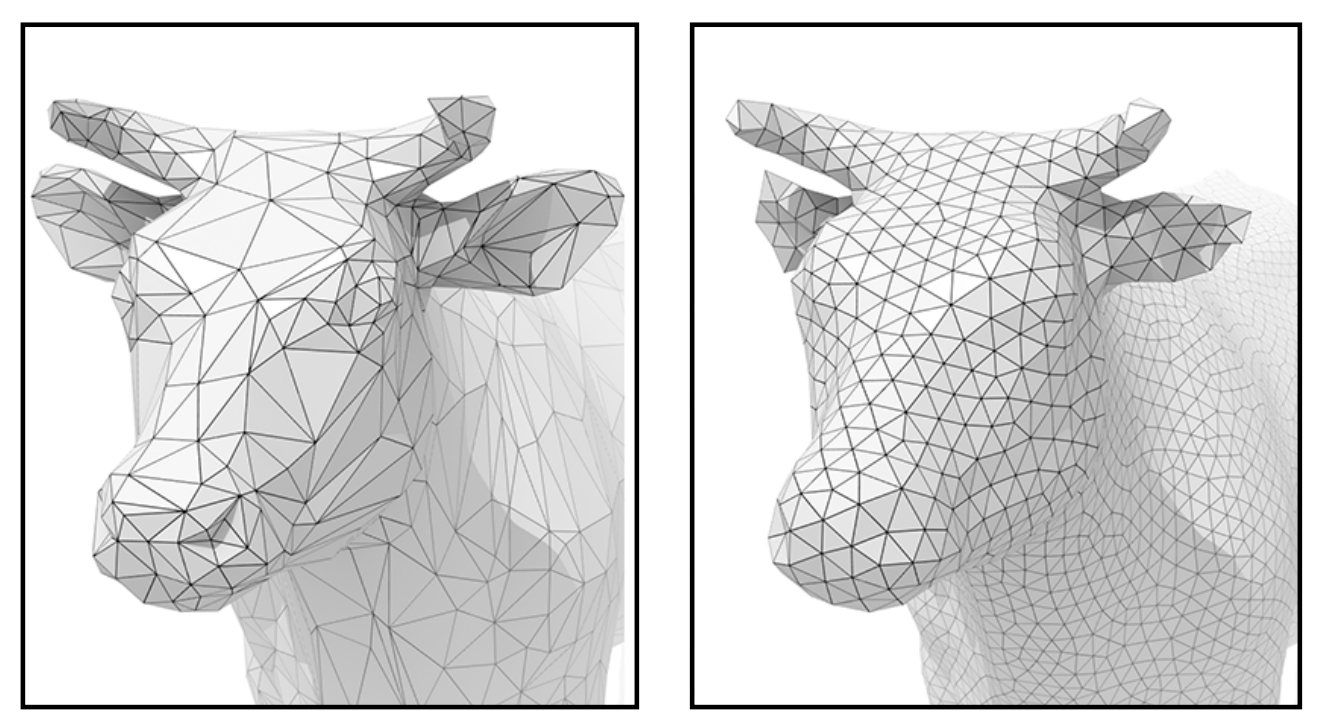
Mesh subdivision(细分)
讲到了两种细分方法,Loop Subdivision & Catmull-Clark Subdivision。
总的来说,引入了更多的几何形状,并使物体表面更平滑。
Loop Subdivision(只能处理网格有且只由三角形组成的情况)
主要可以分成两部分:
将一个三角形分成四个
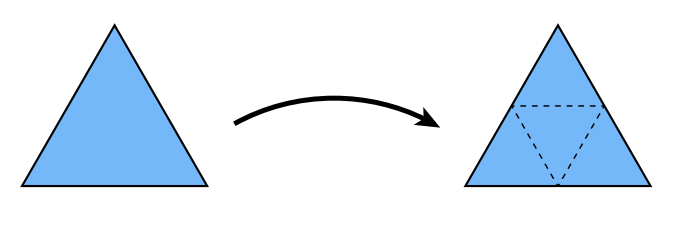
区分新/老顶点,并移动其位置
对于新顶点
找到顶点所在边的两个三角形,其位置由这两个有公共边三角形的四个顶点决定。
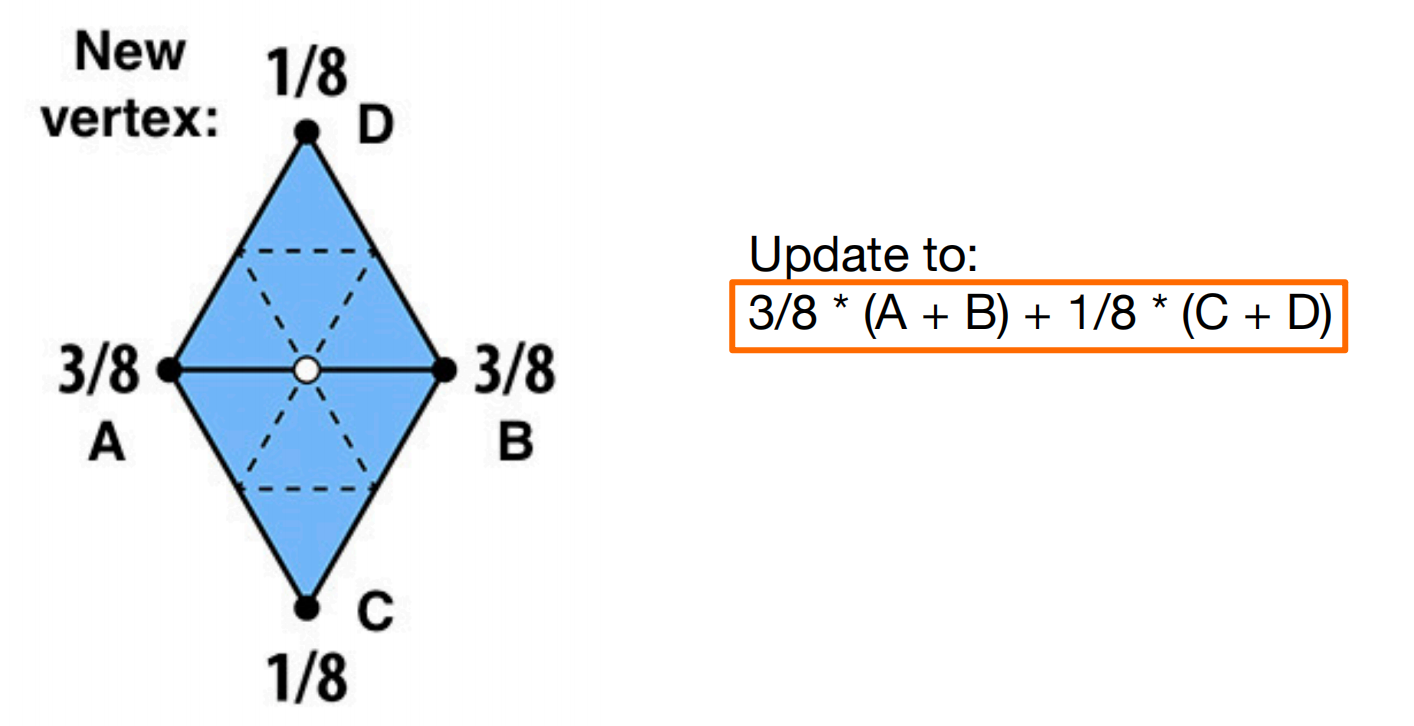
对于老顶点
找到以老顶点为其中一个顶点的所有三角形。其位置由老顶点自己和其他的顶点决定
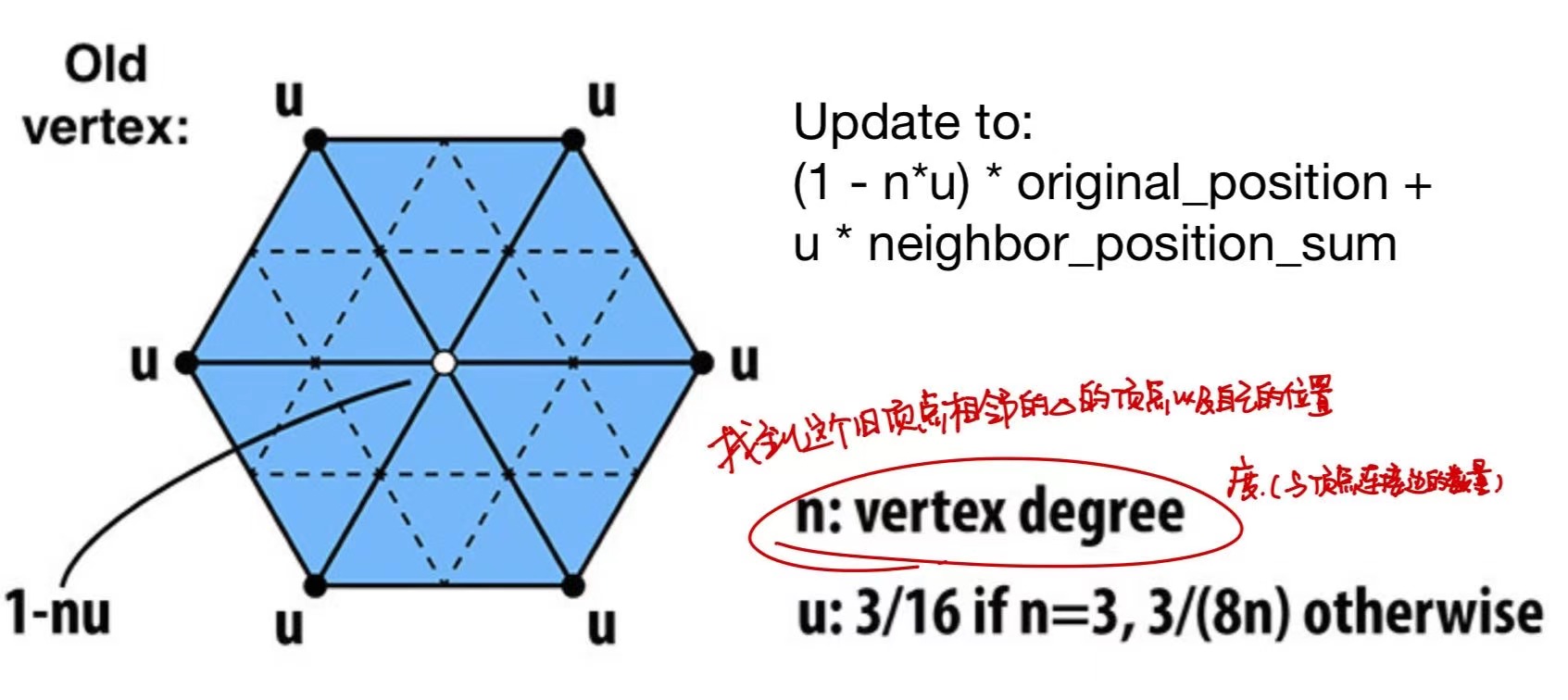
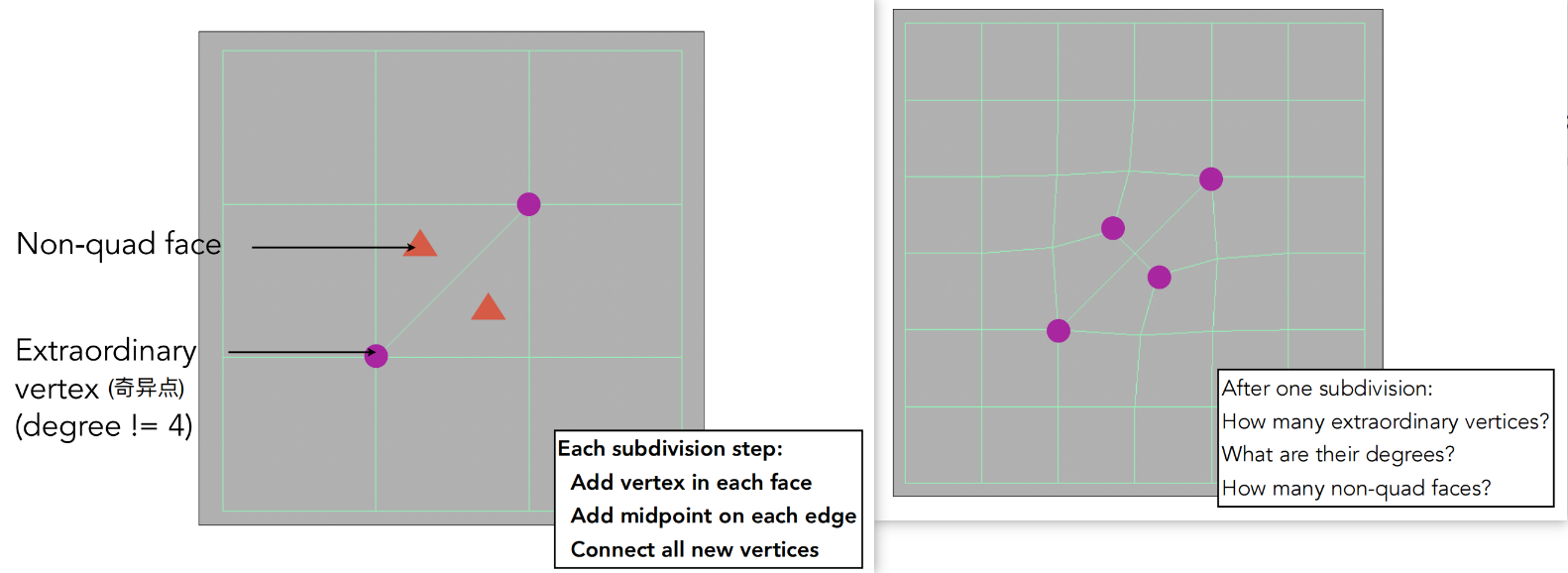
Catmull-Clark Subdivision(能够处理任何形状的网格)
奇异点:度(degree)不为4的顶点(也就是连接边数不为4的顶点),在这里奇异点的个数和非四边形面的个数有关。
步骤:
- 每一条边取中点,每一个面取中点
- 在每一个面中,将面的中点分别和边的中点连线
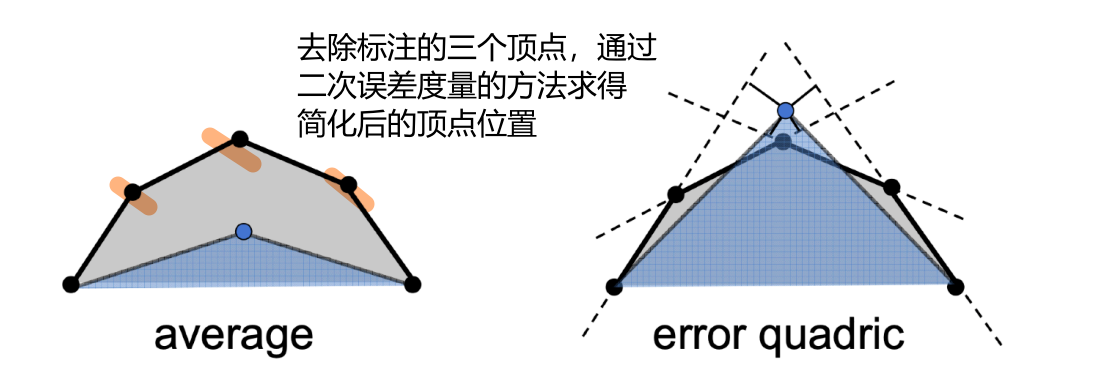
Mesh simplification
可以对比纹理映射,但是处理网格简化问题有一定的难度(如何实现平滑的过渡?)
简化方法:边坍缩(edge collapsing),通过二次误差度量(quadric error metrics,点到相关联的边距离的平方和最小)的方法实现
步骤:
先对所有的顶点求二次误差度量值,使用贪心算法,从最小二次二叉度量结果的顶点开始坍缩;并且需要实时更新顶点对应的值(使用堆或者优先队列等数据结构实现)
Mesh regularization(正则化)
将三角形变为正三角形,便于渲染。
曲线 & 曲面
Bézier Curves
曲线的绘制算法:de Casteljau Algorithm
$$
b^n(t)=\sum_{j=0}^{n}{b_jB_j^n(t)}
$$
$$
B^n_i(t)=\ \left(
\begin{matrix}
n \
t
\end{matrix}
\right)t^i(1-t)^{n-i}
$$
一些特性
曲线的起点和终点就是给出控制点的起点和终点
在有四个控制点的情况下(绘制三次贝塞尔曲线 cubic Bézier curves)
b’(0) = 3(b1 - b0); b’(1) = 3(b3 - b2)
曲线在通过仿射变换后的结果是和重新根据仿射变换后的控制点生成的结果是一致的!
故,只需要将控制点应用变换重新生成即可!
但是,投影变换并不适用。
凸包性(convex hull property)
生成的曲线在控制点围成的凸多边形内
Piecewise Bézier Curves
将多段的Bézier curves连接起来,一般是cubic Bézier curves(也就是控制点为四个的情况)。
C0连续
两段贝塞尔曲线连接在一起(一个控制点是相同的)
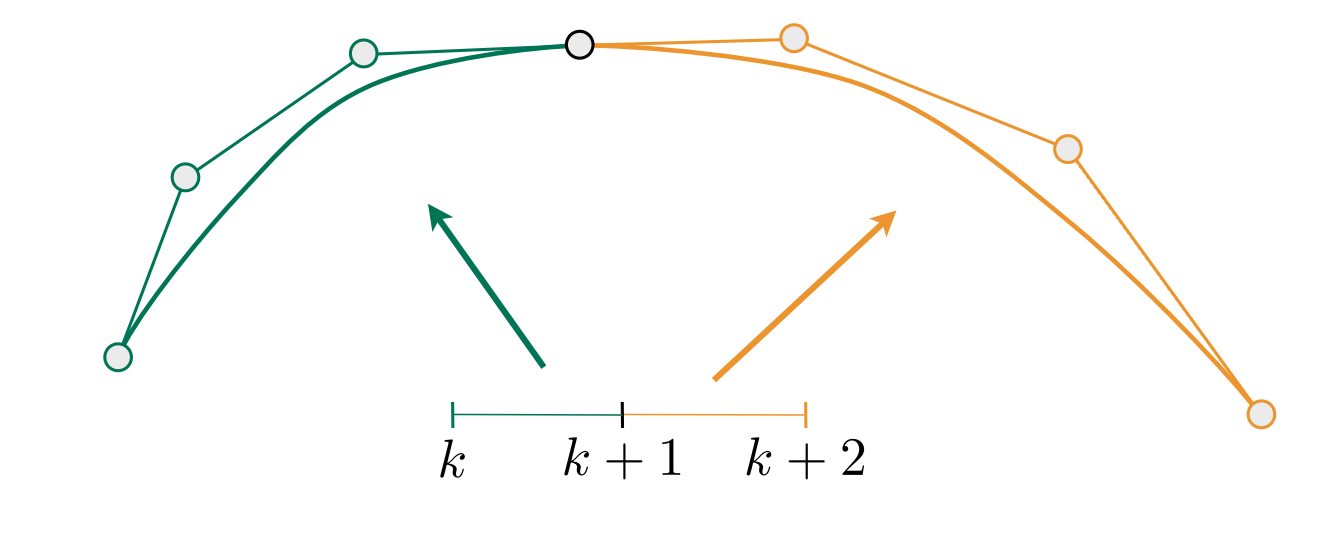
C1连续
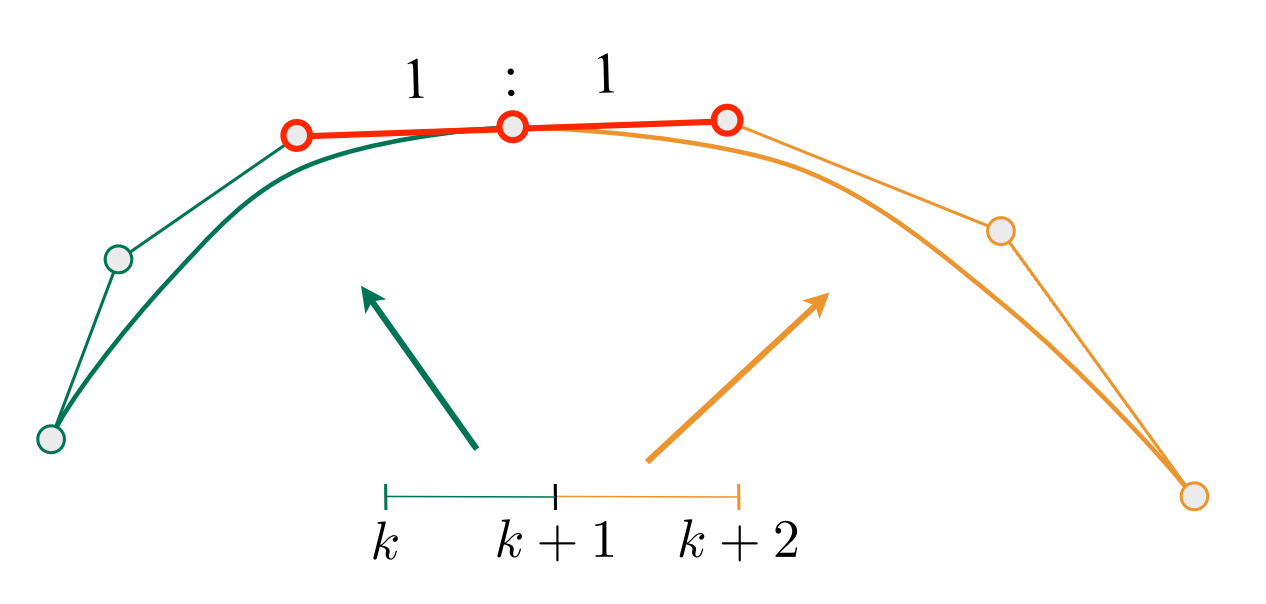
两段贝塞尔曲线是平滑连接的(连接处控制点附近一阶导连续)
需要满足:
① 方向相反;②共线;③等距;
B-splines
B样条,具有局部性的性质,在移动某一个控制点时,只影响曲线的一部分而不是影响全局。
Bézier surfaces
插值(u, v)两个方向上的贝塞尔曲线,形成曲面。