games101课程笔记07-Shading

在这门课程中，shading被定义为对不同物体应用不同材质的过程。并且，shading具有局部性（不考虑其他的物体的作用，所以是没有阴影的）

Blinn-Phong Reflectance Model

光照模型考虑的是对单物体上的单个像素点（shading point）的着色。

diffuse reflection

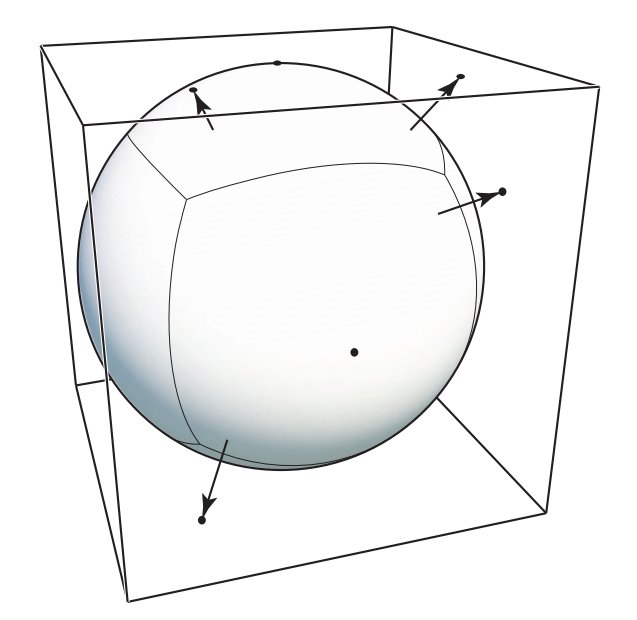
打到物体的光被平均分散到各个方向上。所以，从不同的角度看，漫反射的亮度应该是相同的。

可以得到这样的经验公式：
$$
L_d=k_d(I/r^2)max(0,n·l)
$$

• kd：漫反射系数（表示物体的材质/当前 shading point 的颜色）
• I/r^2：在单位面积上可以接收到的光的能量（单位面积上接收到的能量与r^2成反比）
• max(0, n·l)：法线向量和光线向量的点积，表示当前的单位面积可以接收到的能量的百分比；由于仅考虑反射，所以这个结果是大于0的，当等于0时，表示的颜色为黑色。

specular highlights

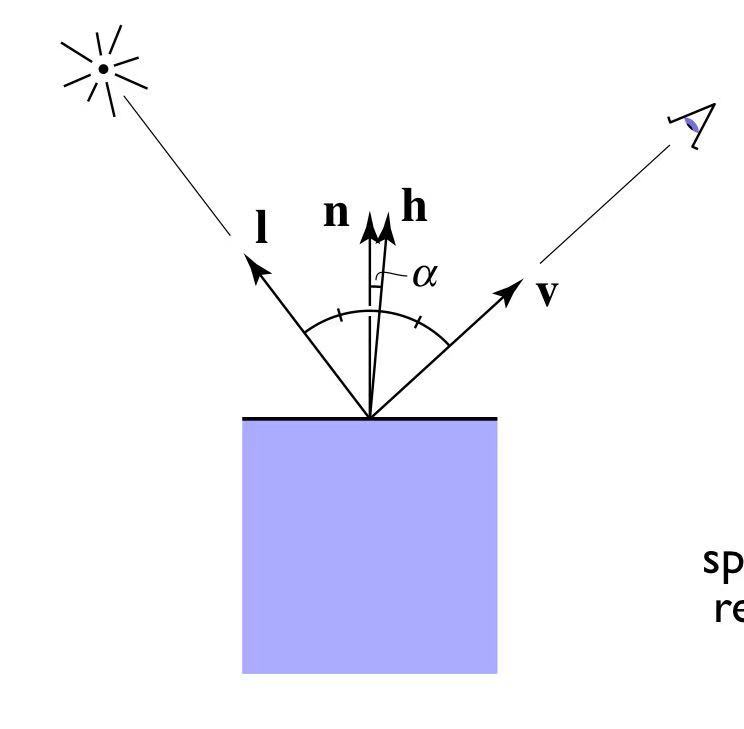
高光通常表现为当观察方向和镜面反射方向逼近时显现（Phong） => 也就是说当半程向量和法向量逼近时显现（Blinn-Phong）

可以得到这样的经验公式：
$$
h=bisector(\vec{v},\vec{l})=\frac{\vec{v}+\vec{l}}{|\vec{v}+\vec{l}|}
$$

$$
L_s=k_s(I/r^2)max(0,cos\alpha)^p=k_s(I/r^2)max(0,\vec{n}·\vec{h})^p
$$

• ks：高光系数（表示物体的材质/当前 shading point 的颜色）
• max（0, n·h）：表示法线向量与半程向量的逼近程度
• p：控制高光的范围，p越大，高光的范围越小

ambient reflection

认为环境光与观察的角度是没有关系的，并且每一个 shading point 接收到的环境光的强度也是相同的，可以得到这样的经验公式：
$$
L_a=k_aI_a
$$

all in all

总之，Blinn-Phong 着色模型可以表现为这样的经验公式：
$$
L=L_a+L_d+L_s=k_aI_a+k_d(I/r^2)max(0,\vec{n}·\vec{l})+k_s(I/r^2)max(0,\vec{n}·\vec{h})^p
$$

Shading Models/Frequencies

flat shading

对三角形面片着相同的颜色

gouraud shading

对三角形面片三个顶点着色并插值

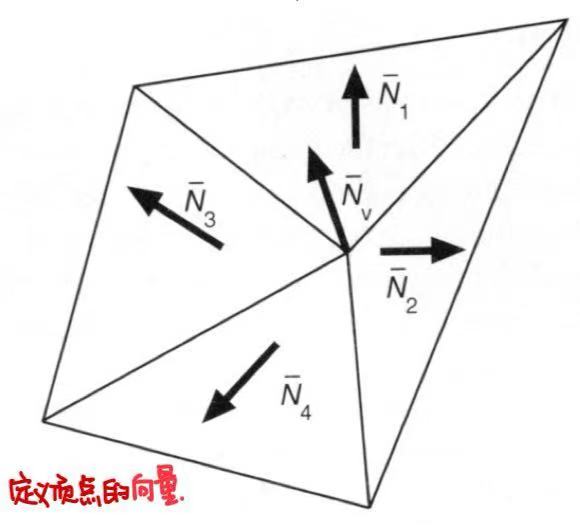
• 顶点的向量的定义：对四周三角形面片的向量求均值
• 

phong shading

对三角形面片上的各个 shading point 着色

• shading point 的向量定义：通过重心插值顶点向量得到

Graphics（Real-time Rendering）Pipeline

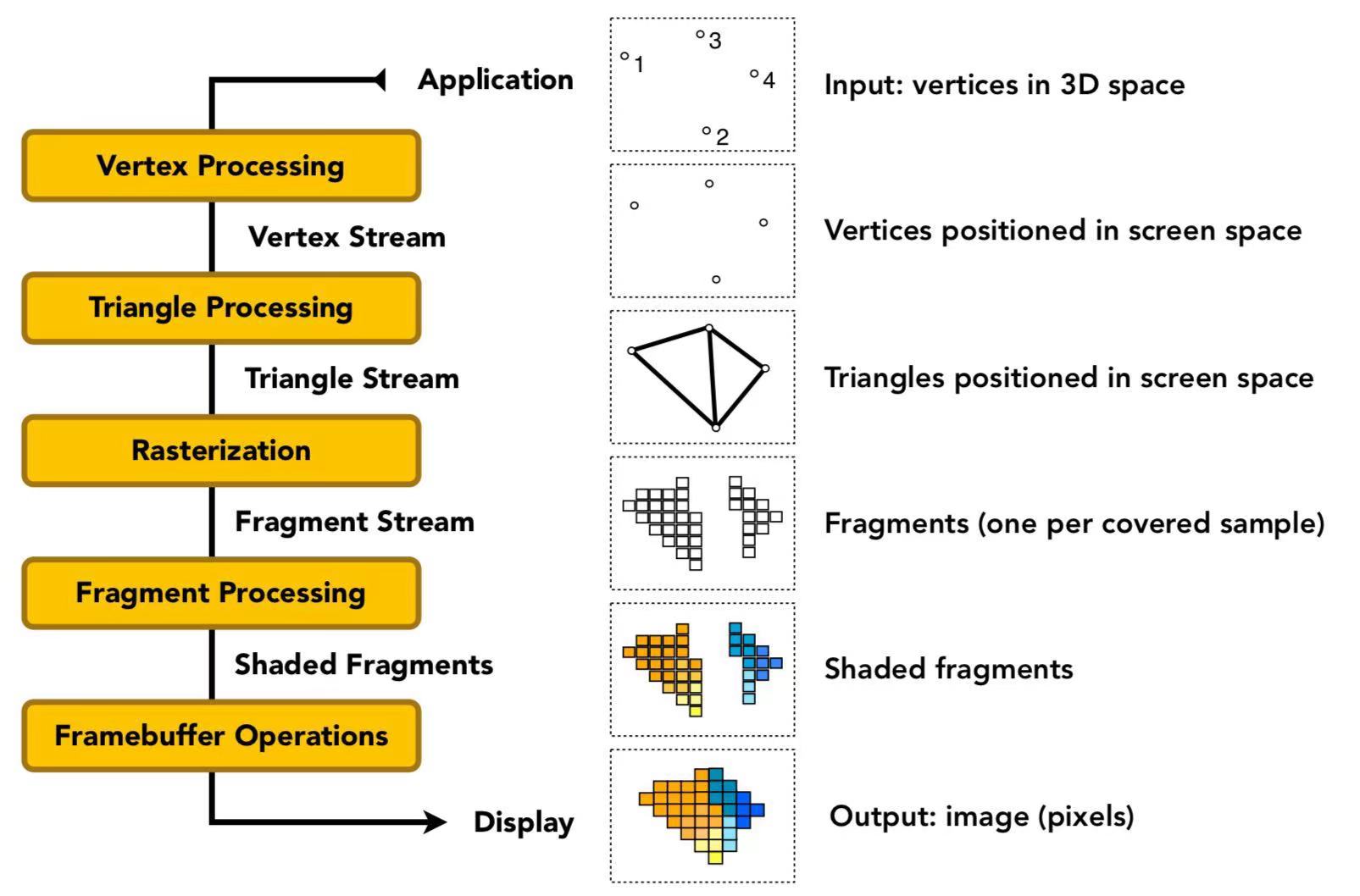
tips:

根据不同的渲染频率，纹理映射、着色等步骤可以选择在Vertex Processing和Fragment Processing两个步骤中完成。

Texture Mapping

将物体的坐标映射到纹理图上的对应位置。

用专业一点的话说，是将画面上的像素(pixel)与纹理上的像素(texel)对应。

纹理图用uv坐标表示（0 <= u <= 1 , 0 <= v <= 1）

简单的纹理映射：应用在漫反射中

for each rasterized screen sample (x, y):
	(u, v) = evaluate texture coordinate at (x, y)
	texcolor = texture.sample(u, v);
	set sample's color to texcolor; // 一般是赋值给漫反射系数 Kd

Texture Magnification

纹理过小时

解决办法：

Bilinear（双线性插值）：当前像素的属性值由邻近的四个顶点插值得到

纹理过大时

会产生严重的走样情况（锯齿jagglies和摩尔纹moire）。信号变化过快，采样频率跟不上导致的。

方法一：对映射的结果应用超采样（supersampling），但是costly！

方法二：MipMap（快，不准的，仅限正方形的范围查询方法）

增加了1/3的开销。

将相邻像素点在映射后的相对距离变化近似为该像素的边长，映射到对应的纹理层。

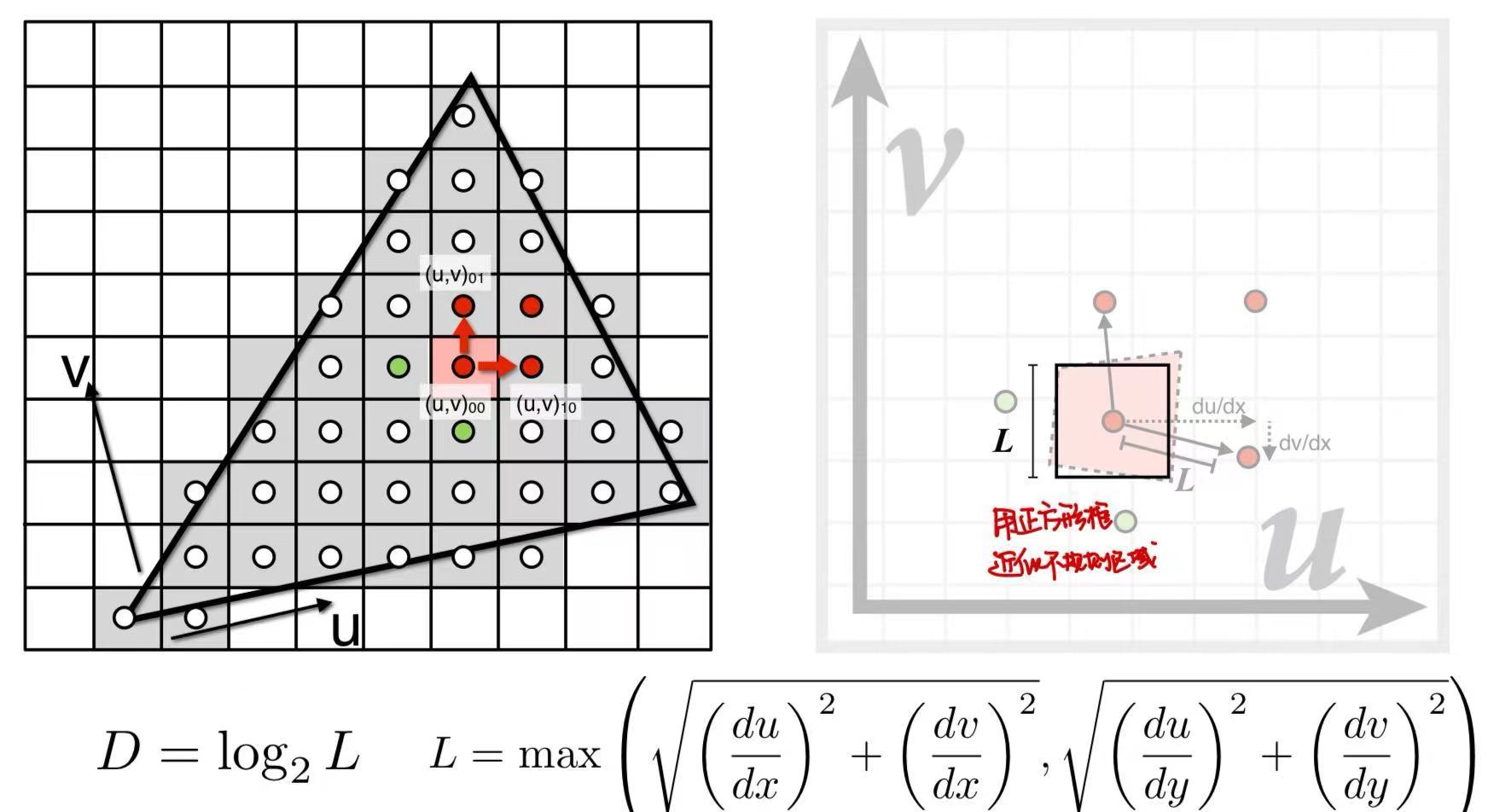
mipmap的问题：

当像素对应的纹理区域不是呈现一个正方形的形状时，会导致纹理映射不合理。

方法三：Trilinear Interpolation

对当前像素点在相邻两层中的纹理映射结果再进行一次插值（避免了计算得到的结果不是正好对应mipmap层中变长的情况，导致映射后的纹理错位）

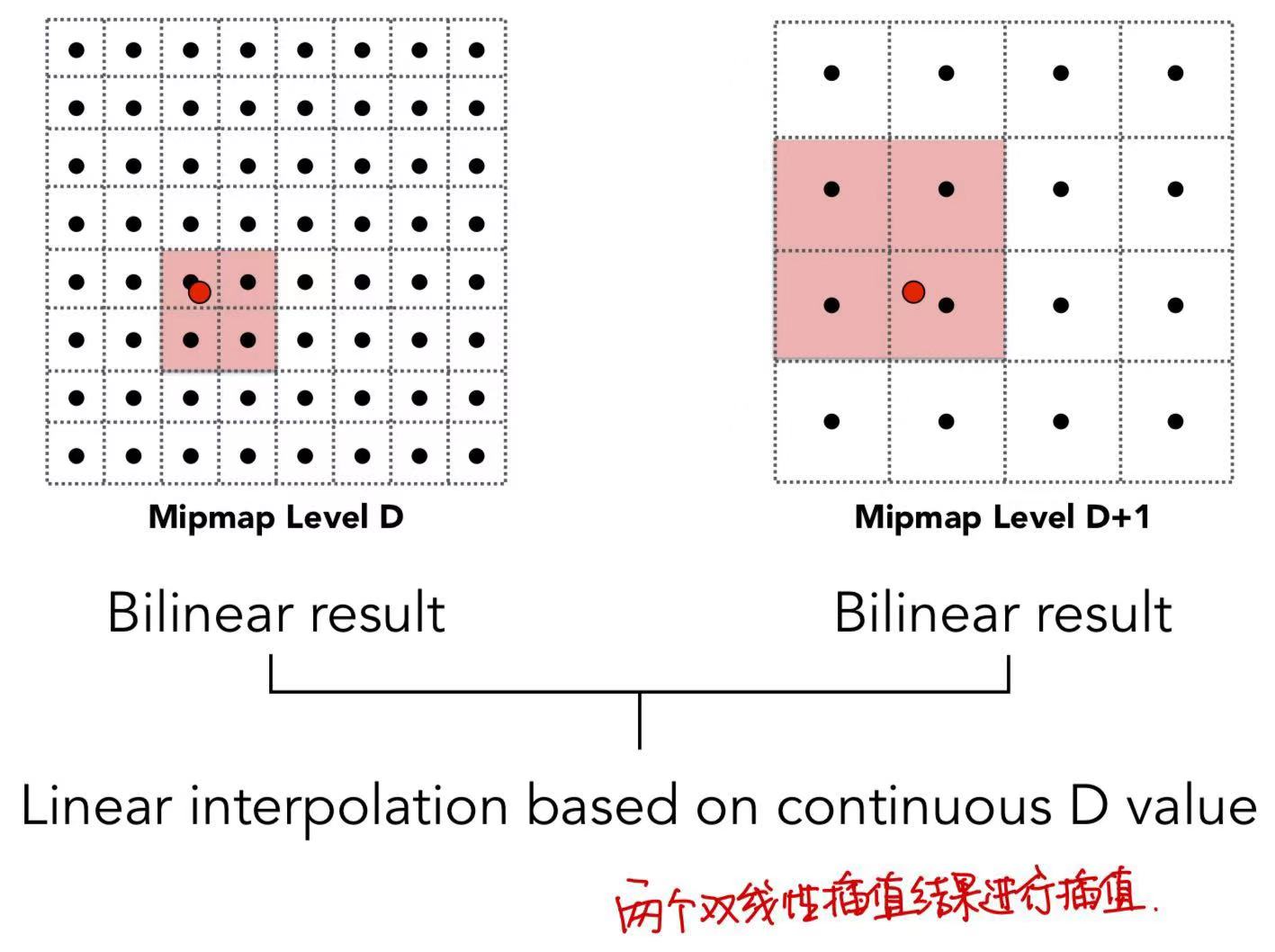
方法四：Aisotropic Filtering（各向异性过滤）

增加了3倍的开销。各向异性过滤数值可以开n倍，表示在原图的基础上生成几层小图，最终收敛到3倍的开销，综合来说只要显存顶得住开销是不大的。

综合考虑了长条形的纹理映射情况。

方法五：EWA filtering

使用多次查询的方法。

Applications of textures

1. environment map 映射环境纹理

• 犹他茶壶（经典模型）

  

• environmental lighting

  用于渲染真实的光照环境

• spherical environment map

  类似鱼眼镜头的纹理映射

  存在的问题：在边缘部分存在扭曲的现象，而且大小比例存在问题（例如，世界地图）

  解决办法

  • cube map

    将球心到球体上点的连线映射到相切的立方体上

    

    这种情况下，通过立方体的六个面描述不同方向的光照信息（也就是将球面均匀分成了六等分，扭曲的现象得到缓解！）

1. 纹理也能影响shading

• bump mapping vs displacement mapping

  纹理可以定义任意不同位置点的属性

  两个方法的输入是相同的，都是一张纹理图，期望对顶点进行怎样的扰动

  bump mapping

  • 不改变点的几何信息（位置信息等都没有改变）
  • 仅扰动表面上每个点的法向量（改变相对高度）
  • 问题：①在阴影复杂/物体边缘的情况下会不真实

  displacement mapping

  • 对表面上任意点的进行移动操作。
  • 问题：① 要求模型足够精细以跟上纹理的采样频率
    • 在DirectX中采用了动态曲面细分的功能
      • 初始状态不是非常精细的模型
      • 但是会根据实际的需求进行曲面细分细化模型

• 3d procedural noise + solid modeling

  使用3维空间噪声函数定义纹理

• provide precomputed shading

  渲染静态场景的时候，可以将阴影图（ambient occlusion texture map）存储起来，节约渲染时间。

• 3d textures and volume rendering

  体积渲染

  常见用于x光扫描等场景。

Shadow Mapping

只能处理点光源（生成硬阴影）。

步骤

做两趟光栅化操作，进行深度对比。

1. 从光源出发，记录深度图
2. 从视点出发，将映射到的点重新投影回光源，比较映射到的点的深度和对应的深度图里记录的深度是否一致

存在的问题

• 受到深度图分辨率的影响（深度图分辨率过低）

• 深度比较涉及到的浮点数比较问题

  一般采用做差比大小、加一个偏差（bias）

附录：Barycentric coordinates

重心坐标

通过重心坐标插值，可以用三角形三个坐标的线性组合表示内部任意一点的属性，实现平滑过度的效果！

满足点(x, y)在三角形内的条件

1. $$
   (x,y)=\alpha A+\beta B + \gamma C
   $$

2. $$
   \alpha + \beta + \gamma = 1
   $$

3. $$
   \alpha,\beta,\gamma>=0
   $$

重心坐标具体系数的求值

• 任意一点的重心坐标可以通过面积比（三角形三个顶点对面的不相邻的三角形）求出

  

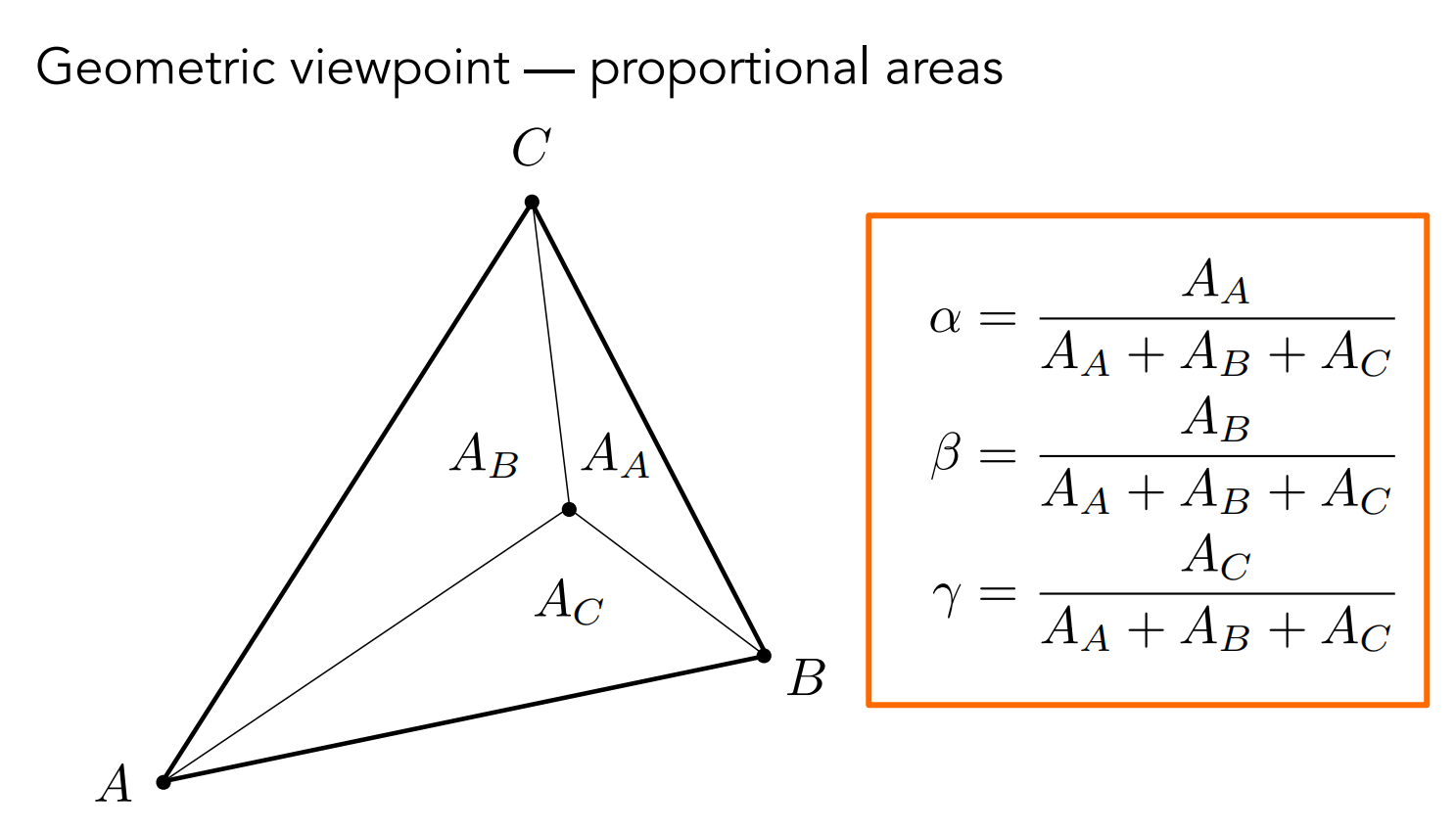
• formula

  

使用重心坐标需要注意的问题

经过投影变换之后，重心坐标的表示会发生变化。

解决方法：在变换之前插值三维的坐标值，而不是在投影变换后对二维的坐标进行插值。