games101_hw1

hw1中使用矩阵表示变换过程的数学推导过程。

MVP变换

modle矩阵

模型变换的任务是要让物体放入视景体内。

在这个hw中，是通过绕z轴的旋转实现的。

view矩阵

视图变换的任务是要调整视图的位置，使物体在成像的中间位置。

通过调整视点的位置实现。

projection矩阵

投影变换的任务是先把投影变换的视景体改为正交变换的视景体（将四棱柱的底面和侧面向内压缩），然后对视景体进行正交投影变换，投影为NDC坐标系上的图像。

提供的参数有视角fov，宽高比aspect_ratio，近平面n，远平面f。

• 改变视景体的矩阵

  1. 按照特殊到一般的思想，先寻找同一切面上的点的关系（变换后两个点在x轴上的坐标是相同的）

     

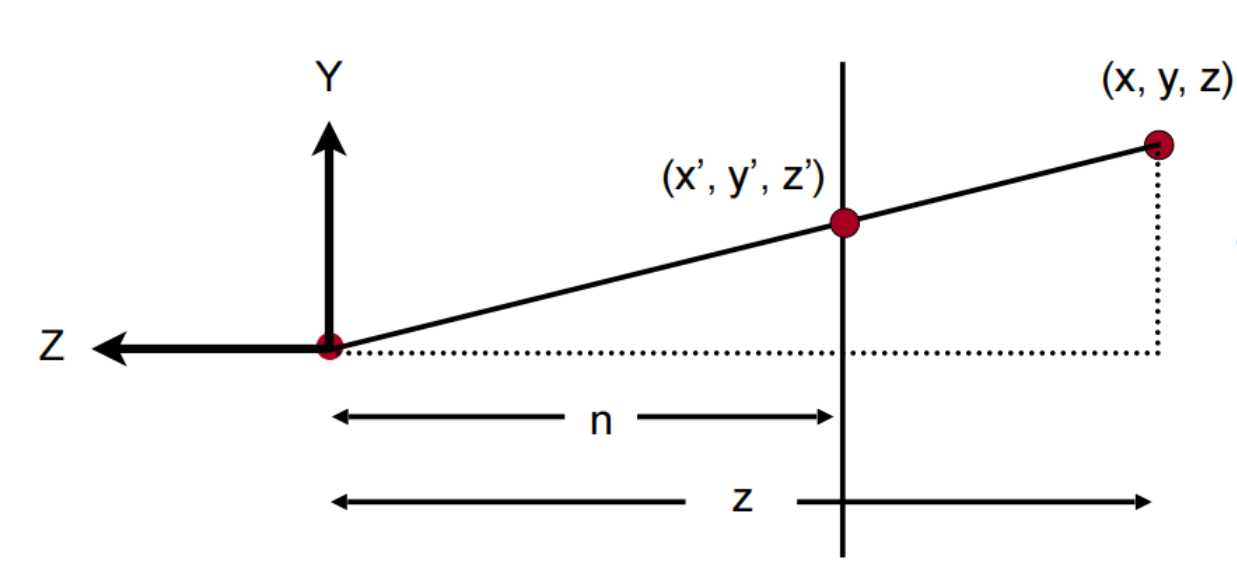
     可以得到
     $$
     y’=\frac{n}{z}y
     $$
     同理，可以得到
     $$
     x’=\frac{n}{z}x
     $$
     在齐次坐标系下，使用第一步变换矩阵，可以使
     $$
     坐标 (\begin{matrix} x \\ y\\ z \\ 1 \end{matrix}) 变换为 (\begin{matrix} nx/z \\ ny/z \\ z’ \\ 1 \end{matrix})，也就是(\begin{matrix} nx \\ ny \\ z’z \\ z \end{matrix})。
     $$

  2. 通过这个表达式，可以猜出一些这个4*4变换矩阵的参数，也就是

     ​
     $$
     M_(persp→ortho)=(\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ a & b & c & d \\ 0 & 0 & 1 & 0 \end{matrix})
     $$
     还剩第三行的参数还没有得到，就要做到了！

  3. 可以得到 z'z=ax+by+cz+d，根据常识可以得到 x 和 y 的坐标值对 z 是没有影响的，故 a=0, b = 0。

     所以剩下的就是 z'z=cz+d。

  4. 根据解方程的思想，有两个未知数，就得要两个方程才能解。

     由于，顶点在近平面和远平面上时，变换后 z 坐标是不会变的（z'=z），故进行带入。

     $$
     n^2=cn+d ① \\
     f^2=cf+d ②
     $$
     联立，解得
     $$
     c=n+f, d=-nf
     $$

  5. 也就是说！视景体变换矩阵为：

     $$
     M_(persp→ortho)=(\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{matrix})
     $$

• 正交投影变换矩阵

  这一个变换矩阵需要将长方体的视景体压缩为边长为1的立方体，并且这个立方体的中心为世界坐标系的原点。

  1. 可以求得视景体的高h为 h=n*tan(fov/2)*2，宽w为 w=h*aspect\_ratio，深度z为 z=f-n（注意这里的符号，z是指向负方向的）。

  2. 故，可以得到正交投影的变换矩阵为：

     $$
     M_ortho=(\begin{matrix} 2/w & 0 & 0 & 0 \\ 0 & 2/h & 0 & 0 \\ 0 & 0 & 2/z & -(n+f)/2 \\ 0 & 0 & 0 & 1 \end{matrix})
     $$

视口变换

简单来说，是调用了void rst::rasterizer::draw(rst::pos_buf_id pos_buffer, rst::ind_buf_id ind_buffer, rst::Primitive type)这个函数，先绘制三角形的三个顶点，然后进行连接。

• 绘制顶点

  1. 对存储的顶点应用MVP变化矩阵

  2. 对顶点进行屏幕空间转换

     • 这里对每一个顶点进行了深度值偏移的操作，具体代码为：

       // 深度值缩放
       float f1 = (100 - 0.1) / 2.0;
       float f2 = (100 + 0.1) / 2.0;
       //....
       for (each vert){
           //....
           vert.z() = vert.z() * f1 + f2;
       }

       f1 和 f2 的作用是将深度值 $$z$$ 从 [-1, 1] 的归一化设备坐标范围映射到设定的深度范围内（比如 [0.1, 100] ）

       • 首先，将归一化深度值 vert.z() 乘以缩放因子 f1，将深度值的范围从 [-1, 1] 扩展到 [-49.95, 49.95]。
       • 然后，加上 f2 进行偏移，使范围变为 [0.1, 100]。

  3. 绘制顶点

• 连接

  • 使用插值的方法

PS. 绕固定轴旋转

具体思路：先将轴转到与z同方向，然后转动角度angle后，再将轴转回去。

假设轴为Vector3f axis，转动角度为angle

计算将轴转到z方向的矩阵可以分解为两步：先将轴转到zOx面上（绕x轴），然后转到z轴上（在xOz面上转动）

1. 可以得到转动角度为：
   $$
   tan(\theta)=axis[1]/axis[2]
   $$

2. 同理，可以得到第二步的转动角度为：
   $$
   sin(\alpha)=(-1) * axis[0]
   $$