games101课程笔记05-Rasterization

在课程中，假定一个像素表示一个纯色的方块（；´д｀）ゞ

viewport transformation（视口变换）

屏幕

• 由像素点构成
  • 在这门课程中，像素定义为纯色的小方块，由三原色混色成
• 离散的
• 二维的

屏幕空间（视口变换）

• 像素的坐标为整数的x, y
• 像素坐标表示范围是(0, 0) - (width - 1, height - 1)
• 像素(x, y)表示的是像素的中心(x + 0.5, y + 0.5)
• 屏幕覆盖的范围是(0, 0) - (width, height)
• 忽略z轴
• 将小方块上的坐标由[-1, 1]^2映射到[0, width] * [0, height]

光栅化

将三角形作为基本的形状

• 三角形是最基本的多边形
• 能够构成其他的多边形
• 一定是在一个平面上
• 有完善的插值方法

经典问题：如何判定一个点在三角形内：叉积！

如何优化判定性能：

• 使用包围盒，减少遍历范围
• Incremental Triangle Traversal（增量三角形遍历？）适用于细长和经过旋转的三角形。
  • 计算得到每一像素行里最左端和最右端的像素点。

反走样！

采样理论

采样被广泛应用在计算机图形学中（光栅化），不仅可以对不同的位置进行采样，也可以对不同的时间片进行采样。

采样过程中产生的不希望的东西被称为sampling artifacts，通常为锯齿（jaggies）、摩尔纹（moire）、马车车轮错觉（wagon wheel illusion）等。

产生这种sampling artifacts的原因是信号改变过于快，但是采样频率过低导致的。

频域

傅里叶变换使用正弦函数和余弦函数逼近某一个函数的过程，其中，这些正弦和余弦函数代表不同的频率。

通过傅里叶变化及其逆变换，可以实现在时域和频域之间的转换。

其中，采样的频率应该要与函数的频率相匹配，否则就会出现走样（aliases）的情况，即是用同样方法采样不同频率函数，得到的结果完全相同。

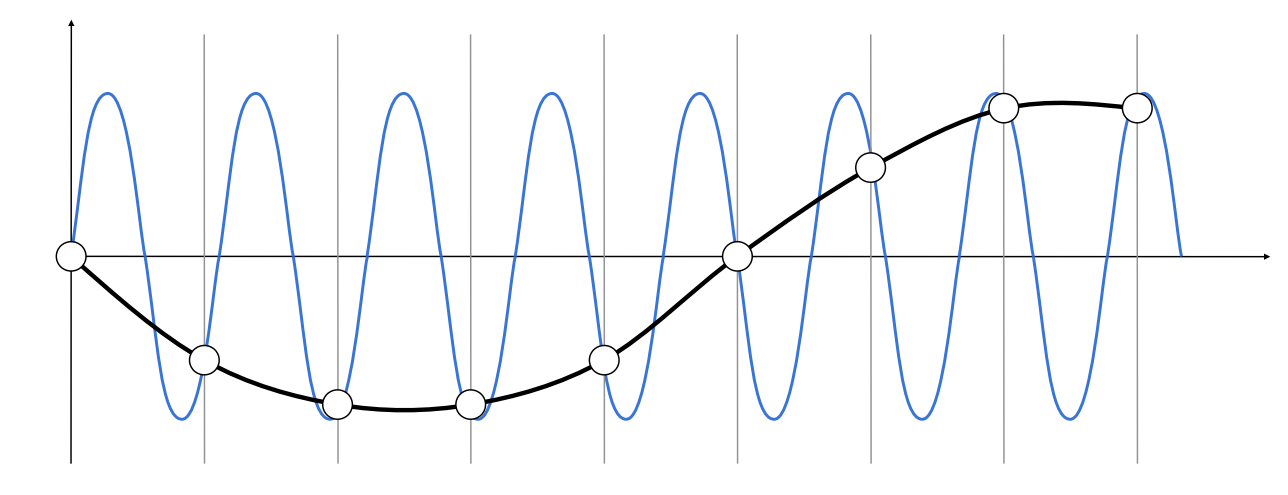
滤波

滤波，就是去除某些频率的内容。

高通滤波（high-pass filter）：只剩下高频信息，对应在时域中只剩下边界信息（线条两侧发生畸变的部分）

低通滤波（low-pass filter）：只剩下低频信息

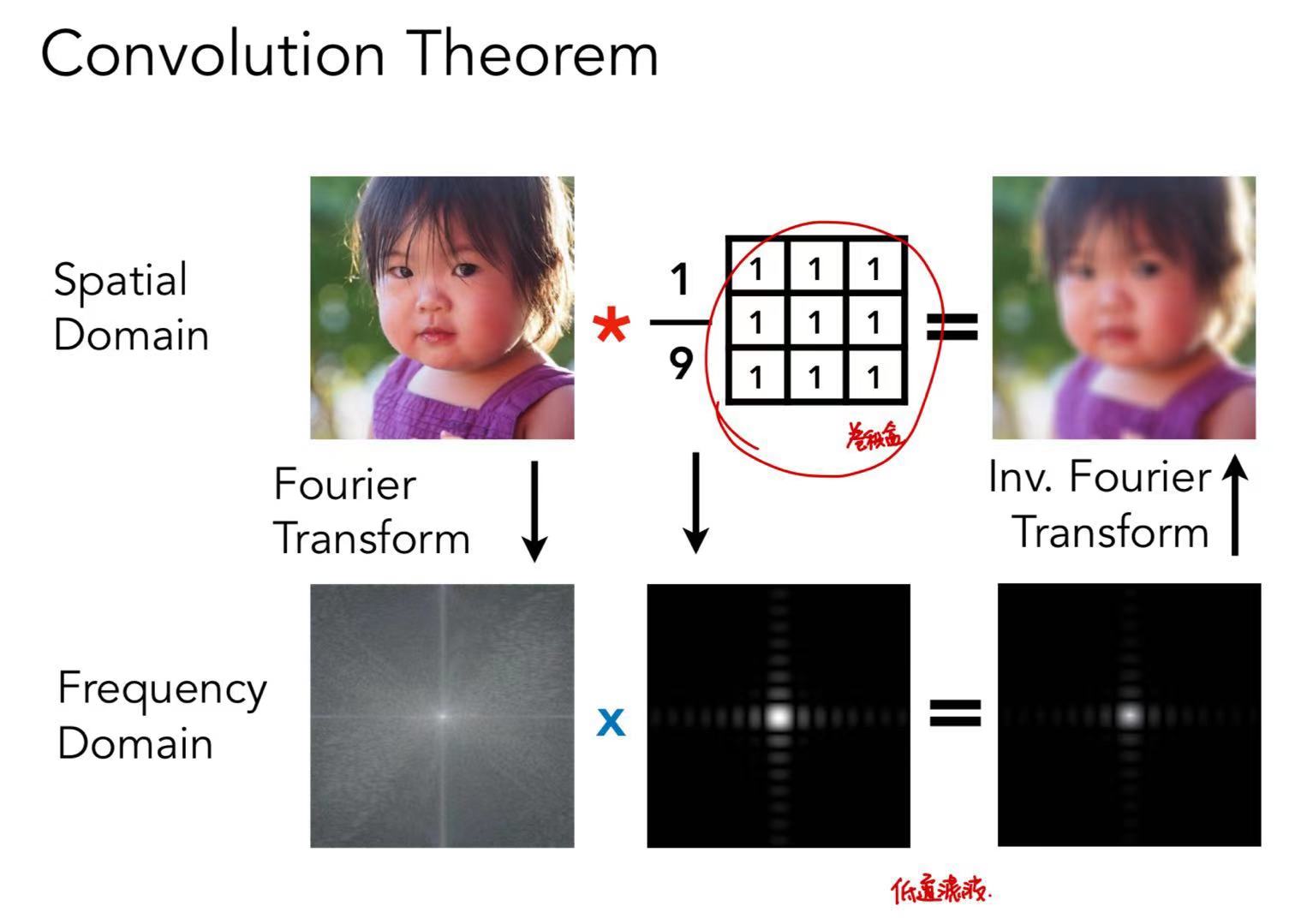
滤波 = 卷积 = 求平均值。

对物体对应时域的卷积 = 对物体对应频域的乘积，反之 对物体对应时域的乘积=对物体对应频域的卷积 也成立。

如图所示，对图像做卷积的过程也就是在去除图像的高频信息，最终结果是变得模糊。

如何减少sampling artifacts

1. 增加采样率

2. 反走样

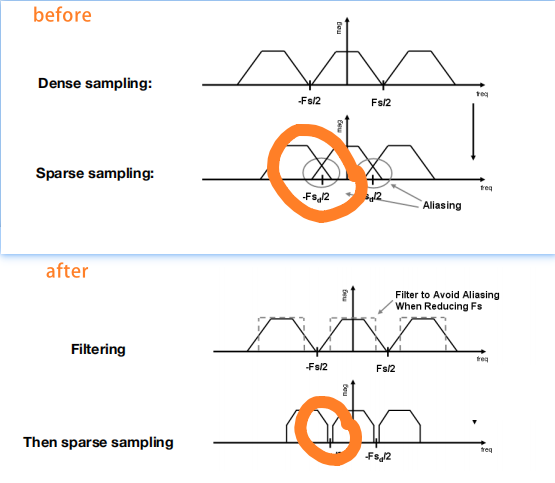
   • 去掉图像的高频信息再采样。

     如图所示，再滤波后，因为采样频率低造成的频谱混叠现象就不存在了。

     

反走样的方法

• MSAA（Antialiasing By Supersampling）超采样

  将一个实际的像素划分为多个虚拟的小像素进行采样，开销很大！

  • 超采样（super smpling）和超分辨率（super resolution）本质上是相同的，但不是同一件事情
    • 都是想要从低分辨率变成高分辨率
    • 普遍面临采样频率不够的问题
    • 可以使用深度学习的方法 DLSS（Deep Learning Super Sampling）

• 与时俱进的方法

  • FXAA（Fast approximate AA）

    在硬件上进行改进，FXAA将像素的提取和混合过程交由GPU 内的ALU执行

  • TAA（Temporal AA）

    TAA的原理是利用相机抖动和历史帧信息来增加像素的采样数，广泛应用于引擎中

可见性/遮挡问题（visibility/occlusion）

画家算法（Painter’s Algorithm）

由远及近画物体。

需要对物体根据深度排序，所以时间复杂度为O(nlogn)。

但是不能解决物体重叠的情况。

Z-Buffer

不能处理透明物体的深度！！

思想：

1. 存储屏幕空间上每一个像素上可以采样到的最小深度值。
2. 需要额外的深度缓冲。
   1. 帧缓冲（frame buffer）存储颜色值
   2. 深度缓冲（z-buffer）存储深度值

具体实现：

​ 遍历每一个三角形的每一个像素，如果其深度值为最小值，则更新深度缓冲和帧缓冲对应像素的深度值和颜色值。

复杂度

• z-buffer算法的时间复杂度为O(n)。（只是记录了每一个像素值对应的最小深度，没有进行排序操作）。
• z-buffer算法和遍历三角形的顺序无关（排除同一像素上有相同深度三角形像素点的情况）