games101课程笔记03-Transformation

transformation相关的内容（二维变换、三维变换、viewing 变换）

仿射变换（Affine Transformations）

• 仿射变换 = 线性变换 + 平移（translate）

  • 用一个二维坐标表示二维平面上的点，可以有等式：

    $$
    (\begin{matrix} x’\\ y’\end{matrix})=(\begin{matrix}a & b \\c & d \end{matrix})(\begin{matrix} x \\y \end{matrix})+(\begin{matrix}t_x \\ t_y \end{matrix})
    $$

  • 其中，二维平面线性变换可以细分为：旋转（rotation） + 缩放（scale） + 错切（sheer）

    

• 齐次坐标

  • 向量具有平移不变性（保证向量在经过平移变换后自身保持不变）
    • 2维点 = (x, y, 1)^T
    • 2维向量 = (x, y ,0)^T
  • 向量与点的加减法（当w方向的值为1/0时）
    • 向量 + 向量 = 向量
    • 点 - 点 = 向量
    • 点 + 向量 = 向量
    • 点 + 点 = 两点的中点

3D旋转的表示

• 欧拉角

  

• rodrigues‘ rotation formula

• 四元数

viewing transformation

MVP变换

MVP变换的组成：

• model transformation 模型变换（模型空间 -> 世界空间）

  placing objects

• view transformation/camera transformation 视图变换（世界空间 -> 观察空间）

  placing camera

  一般来说，可以将照相机放在指定位置（pos: 原点；up：Y，look at：-Z），然后移动物体的位置。

  如何将照相机移动到指定位置？第一步，将相机的位置移动到原点；第二步，因为旋转矩阵是正交阵，故可以先写出从原点固定位置到现在位置的变换矩阵，然后求解逆运算旋转矩阵R’。

• projection transformation 投影变换（观察空间 -> 裁剪空间）

projection transformation

• orthographic projection（cuboid to “canonical” cube [-1, 1]^3）NDC坐标系！

  一种可行的理解

  • 照相机处于原点，朝向-z方向，朝上方向为y
  • 去掉物体在z方向上的坐标
  • 通过移动和缩放将结果限制在[-1, 1]^2的矩形内

  P.S. -z方向为z轴的正方向，所以在数值上，近平面 > 远平面

• perspective projection（frustum to “canonical” cube）

  通过寻找特殊值的方式，可以找到将透视投影上的物体转换到正交投影的变换矩阵。

  所以，求解透视投影的方法是先转换为正交投影，然后再根据正交投影的特性进行计算。

  $$
  M_{persp}=M_{ortho}M_{persp->ortho}
  $$
  更进一步地来说，可以分为这两个步骤：

  1. 将四棱台变为长方体。就是把顶面不动，把底面以及侧面向内压缩为一个长方体。
  2. 对长方体进行正交投影变换。

  定义视景体的方式

  • 垂直可视角度 fovY

  • 近平面 zNear，zFar

  • 宽高比 Aspect ratio

    

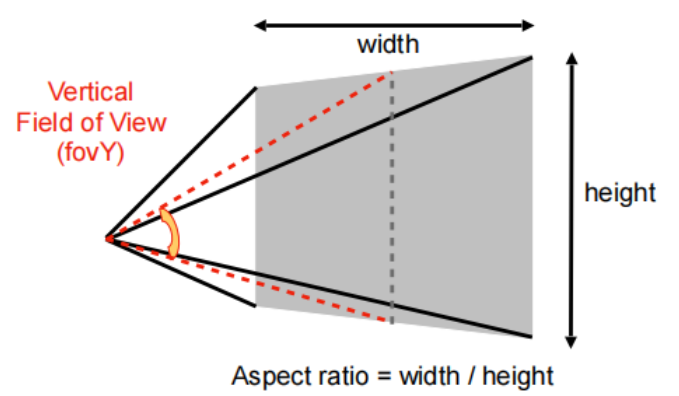
!important

具体的公式推导见hw1笔记

https://blog.poivrehxx.site/2024/10/27/games101_hw1/