代码随想录一刷笔记_动态规划(上)
60+在408的算法考察难度和深度上还是收手了👍)
动态规划理论基础
DP的特点
每一个状态是由上一个状态推导出来的(区别于贪心,贪心是局部选择最优)
DP的解题步骤
确定dp数组(dp table)以及下标的含义(很关键⭐⭐⭐⭐⭐)
这一步,应该是最先得到的,最明显的,就是当下标为 i 的时候题目求得值是多少!然后,再思考一下怎样递推(这个难推敲)实现。
确定递推公式(需要推导一下)
dp数组如何初始化
确定遍历顺序
举例推导dp数组
背包问题
背包问题的分类(只需要掌握01背包和完全背包)
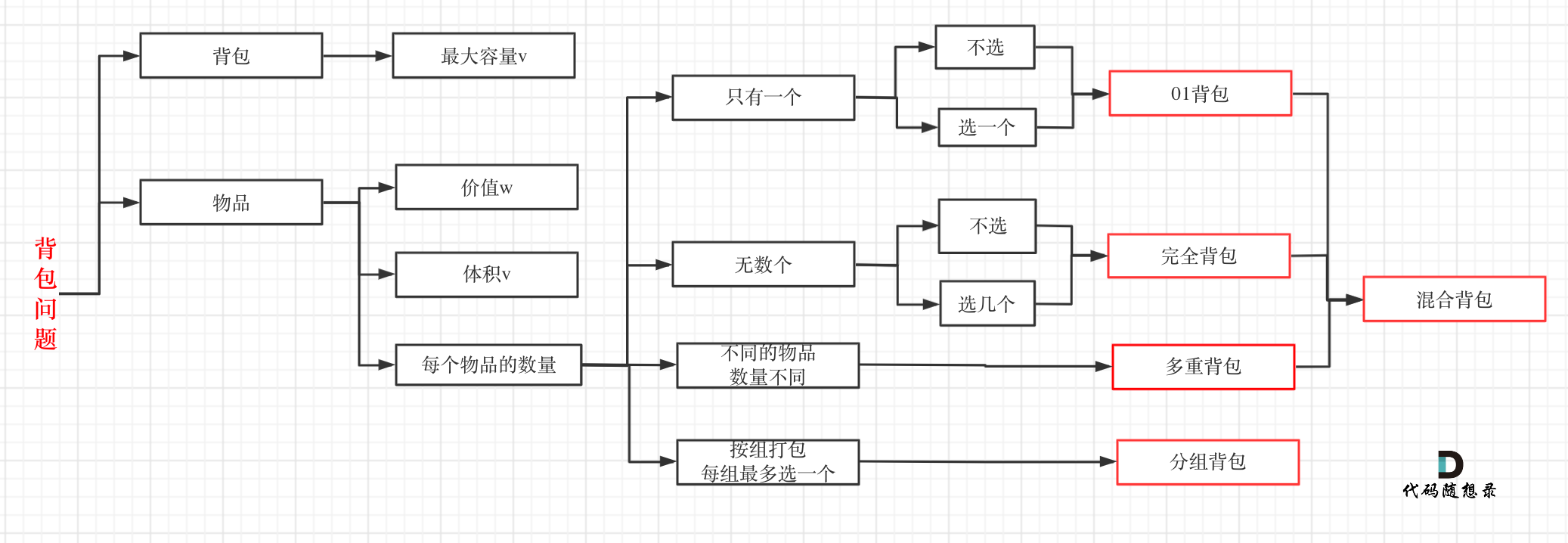
01背包理论基础
问题描述:有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
使用二维数组DP
按照dp的解题步骤考虑背包问题
确定dp数组(dp table)以及下标的含义
这里需要使用二维数组(两个维度分别表示
物品i和背包容量j)确定递推公式(需要演算一下)
当遍历dp[i][j]的位置时,
需要判定
物体重量weight[i]与此时背包容量j的关系:如果可以放入,需要在放入后的总价值(放入这个物体可能需要将前面的一些给取出)和放入前的总价值(记录在对应的上一层中)中取较高者。
表达式为:
1
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);dp数组如何初始化
思考一些递推公式中可能会产生越界问题的位置:也就是第一行和第一列。
其中,第一列表示的是背包容量为0的情况,所以初始化为0即可;而第一行,需要遍历一遍,标注出物品0能够放入的情况。
确定遍历顺序
从左到右,从上到下。
Q&A
Q:遍历背包和遍历物品能否交换次序?
A:是可以的,因为每一次循环中dp[i][j]需要的数据都在二维数组的左上角,不影响结果的表示。
使用滚动数组(一维数组)DP
将二维数组进行压缩,使用一维数组的方法表示,节约了空间。
确定dp数组(dp table)以及下标的含义
使用一维数组,下标
j表示背包此时的容量,dp[j]表示此时可放入的最大物品价值。确定递推公式
当遍历
dp[i][j]的位置时,需要判定物体的重量weight[i]与背包容量j的关系:如果可以放入,需要在放入后的总价值(放入这个物体可能需要将前面的一些给取出)和放入前的总价值里取较高者。
1
2
3
4
5
6
7
8// 外层循环遍历每个类型的研究材料
for (int i = 0; i < M; ++i) {
// 内层循环从 N 空间逐渐减少到当前研究材料所占空间
for (int j = N; j >= weight[i]; --j) {
// 考虑当前研究材料选择和不选择的情况,选择最大值
dp[j] = max(dp[j], dp[j - weight[i]] + values[i]);
}
}dp数组如何初始化
初始化为0即可。
确定遍历顺序
使用两层for循环,其中外层循环按照物品序号遍历物品;
内层循环按照背包容量范围从大到小遍历 [物品的重量,需求的背包容量范围]
Q&A
Q:为什么内层循环要从大到小遍历?
A:为了保证物品i只被放入一次!因为使用滚动数组,上一层循环的数值会被本层的循环覆盖,然后我们的表达式求得的值是和index较小的值相关的,所以从大到小遍历,可以避免较小序号的值先被覆盖的情况。
Q:这里两层循环能否交换顺序?
A:不能!因为使用一维dp遍历的方法需要倒序遍历背包容量;如果将两个遍历顺序反过来,每个dp[j]只会放入一个物品,也就是背包里只会放入一个物品。
完全背包理论基础
问题描述:有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
之前有提到,只要在遍历一维数组的时候,将遍历背包容量的顺序变为从小到大即可!此时,故,也就是说,显然可见,两层循环的顺序是可以交换滴。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
是不是可以认为,只要是从小到大遍历的情况,循环的顺序就是可以交换的?
多重背包理论基础
问题描述:有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
也就是说,每一样物品有有限多个,故,可以将其拆分成多个物品,转化成01背包问题!
509 斐波那契数
递归
先是使用了一下递归
时间和空间复杂度还都挺高的

dp
按照dp的解题步骤顺一下这道题
确定dp数组(dp table)以及下标的含义
dp[i]表示第i个数值
确定递推公式
dp[i] = dp[i - 1] + dp[i - 2];
dp数组如何初始化
dp[0] = 0, dp[1] = 1;
确定遍历顺序
从前往后遍历
举例推导dp数组
举个栗子:0, 1, 1, 2, 3, …
70 爬楼梯
回溯
试了下回溯,这简单题也要插几个超时例子是吧(╯▔皿▔)╯
dp
按照dp的解题步骤顺一下这道题
确定dp数组(dp table)以及下标的含义(确定这个很重要!)
dp[i]表示到达第i层楼梯有几种方法
确定递推公式(需要演算一下)
dp[i] = dp[i - 1] + d[i - 2];
dp数组如何初始化
dp[0] = 1(照顾一下i = 2的情况),dp[1] = 1, dp[2] = 2;
确定遍历顺序
从前往后遍历
举例推导dp数组
举个栗子:1, 1, 2, 3, 4, …
完全背包
将可以踩1or2级楼梯视为物品,然后一共有n层,找出一共有几种组合。这样理解的话,就是一个完全背包问题了。
746 使用最小花费爬楼梯
回溯
太棒了,又超时了┗|`O′|┛
dp
按照dp的解题步骤顺一下这道题
确定dp数组(dp table)以及下标的含义(确定这个很重要!)
dp[i]想从这个台阶出发的低消(最低消费)
确定递推公式(需要演算一下)
dp[i] = cost[i] + min(dp[i - 1], dp[i - 2]);
dp数组如何初始化
dp[0] = cost[0], dp[1] = cost[1]
确定遍历顺序
从前往后遍历
举例推导dp数组
举个栗子:cost为[10, 15, 20]
则对应的dp数组为[10, 15, 30]
62 不同路径
dp
按照dp的解题步骤顺一下这道题
确定dp数组(dp table)以及下标的含义
dp[i][j]到达这个格子的方法有几种
确定递推公式(需要演算一下)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
dp数组如何初始化
dp[0][0] = 0;
确定遍历顺序
从左到右,从上到下遍历
举例推导dp数组
举个栗子:dp[0][1] = 1; dp[1][0] = 1;
tips: 如何声明二维的向量
1 | |
63 不同路径Ⅱ
与62 不同路径相比,只要判断先进行对当前位置是否为障碍物的判断就行了,如果是障碍物就continue。
题解的方法有一点冗余力哈哈。
343 整数拆分
这一题没有想到,看了一下题解。
第一个想法是,要想使拆分的数乘积最大,最好是拆分的几个数字数值上是近似的(从给出的样例中找的规律),然后拆成几个数字的话我认为可能和对数有关系,不过在样例中遇到了反例(11)。
dp
按照dp的解题步骤顺一下这道题
确定dp数组(dp table)以及下标的含义
dp[i]表示在下标为i时候的拆分的最大值。
确定递推公式(需要演算一下)
遍历 j ( 0 < j < table.size())
当拆分为两个数的时候,最大值为:j * (i - j);
当拆分大于两个数的时候,最大值为:j * dp[i - j];
当然,这里的dp[i - j]是由前面遍历过来的,表示的是数值为(i - j)时候的最大值,至少由两个数组成,也就说,这时候起码被拆成了3个数(符合前提,逻辑自证,出院!)
故,递推公式可以表示为:
1
2
3
4
5
6for (int i = 2; i < table.size(); i++) {
for (int j = 1; j < i; j++) {
// 这里比较最大值还比较了dp[i]是因为在遍历过程中将最大值存储在了dp[i]里
dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]);
}
}dp数组如何初始化
dp数组初始化为0即可。
确定遍历顺序
从前往后遍历。
举例推导dp数组
此处省略n字(真的不是杠啊什么的,真的懒了….)
贪心
这个方法正常来说确实是想不到😭😭,需要数学证明(每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!)。
96 不同的二叉搜索树
(第一反应又当成找不同的二叉排序树了,瞧我这记性)….
dp
按照dp的解题步骤顺一下这道题
确定dp数组(dp table)以及下标的含义
表示当有 i 个节点时有 dp[i] 个不同的bst树
确定递推公式(需要演算一下)
如果不考虑头节点的话,那就还剩 i - 1 个节点。
此时,左子树有 j 个节点,右子树有 k 个节点,满足 j + k = i - 1;遍历一遍,求得所有的可能。
1
2
3
4
5for (int i = 2; i < dp.size(); i++) {
for (int j = 0; j < i; j++) {
dp[i] += dp[j] * dp[i - j - 1];
}
}dp数组如何初始化
dp[0] = 1; dp[1] = 1。
确定遍历顺序
从小到大遍历
416 分割等和子集
这一题,很明显体现了“取or不取”的思想,所以是很典型的背包问题。
回溯
数据集不大,先试试回溯。
根据“和是否为偶数”,“和大于一半”、“重复数值”等情况进行了剪枝,还是在一些逆天样例上超时了,还是得用背包写呀。
背包
按照dp的五步想一想该怎么写:
确定dp数组下标及其含义
首先是想一下这里的两个维度:子集的个数对应可以放入背包的物品个数;dp数组的下标i表示当前的容量;
也就是说,我们需要判断当容量i为数组总和的一半时,
i和dp[i]的关系。确定递推公式
第一步确定对应背包中两个维度的关系后,递推公式就可以套用过来了:
1
dp[j] = max(dp[j], dp[j - numms[i]] + nums[i])dp数组如何初始化
初始化为0即可
确定递推顺序
第一层循环从前往后遍历,第二层循环从后往前遍历
1049 最后一块石头的重量Ⅱ
分析一下题目,实际上和416 分割等和子集的路径是一模一样的!
他要做的就是将这个石头数组分为两堆,求最小的差值。
tips:
在返回值上,一半石头的最大容量是dp[sum / 2](并且这堆肯定是最小的,因为此时最大容量是一半),则此时另一半石头的容量就是sum - dp[sum / 2],也就是说,此时的两堆相减的值为sum - dp[sum / 2] * 2。
494 目标和
可以使用回溯做,但是肯定又超时了。
背包问题
这一题很明显又是取/不取的问题。通过数学推导,可以得出:
相加的数、这组数的和与目标大小的关系为:2x1(相加和)= target + sum。
但是这里有一个变式,他是要求多少种可能性,故dp数组的定义需要进行相应的变化。
按照dp的五步想一想该怎么写:
确定dp数组下标及其含义
这里的下标表示的是当背包容量为i时,能够存放i的可能性。
确定递推公式
1
dp[j] = dp[j] + dp[j - nums[i]];dp数组如何初始化
dp[0] = 1。当背包容量为0时,有一种方法,就是一个也不取。
确定递推顺序
第一层循环从前往后遍历,第二层循环从后往前遍历
474 一和零
这一题有两个维度,但是能理解为0-1背包的问题。
需要使用二维的dp数组,维度分别为两个量。
518 零钱兑换
这里的零钱是可以重复取的,所以是典型的完全背包问题。
按照dp的五步曲梳理一下:
确定dp数组下标的含义
当背包容量为
j时,可以凑出当前容量的组合数;确定递推公式
1
dp[j] = dp[j] + dp[j - dp[coins[i] - j]];dp数组如何初始化
dp[0] = 1。可以理解为当容量为0时,有一种方法。
dp数组的遍历顺序
这里是完全背包,所以均为从小到大遍历。
tips
这里有一个遍历过程中相加会溢出的样例,输出直接判为0了;在遇到逆天案例的时候,先别急,放到测试案例里试试。试试就shishi(😵😵)
关于两层循环顺序能否交换的问题!
是不行的!若是先遍历背包容量,将会出现情况的可能再进行一次全排列(求组合)的问题。例如,有{1,5}和{5,1}两种可能。
377 组合总和Ⅳ
如上题所述,将内外循环交换次序就是求组合了。
322 零钱兑换
这一题的话,是要满足能够组成需求的容量且此时排列的数量是最少的。
按照完全背包的步骤顺以下~
按照套路来,还是两层递归,并且是要求得排列,所以内层循环是从小到大遍历的。
dp数组初始化为0即可,表示此时均还没有满足需求的情况。
279 完全平方数
这一题很显然就是完全背包,而且解题步骤和322 零钱兑换完全一致,只不过外层循环的遍历顺序需要改变一下。
139 单词拆分
对于这一题,我的理解是,仍然是完全背包问题。要对放入的物品进行一个组合的操作,并且当前的组合需要满足一定的顺序要求。
回溯(记忆化递归)
这里的题解介绍了一个递归的优化方法,叫做记忆化递归(剪枝小技巧)。
使用memory数组保存每次计算的以startIndex起始的计算结果,如果memory[startIndex]里已经被赋值了,直接用memory[startIndex]的结果。
完全背包
题解的方法是将dp数组赋值为bool类型的向量,将单词裁成多个部分,然后直接考虑每一部分的单词是否在列表里存在(使用unordered_set方法)。