代码随想录一刷笔记_链表

60+在408的算法考察难度和深度上还是收手了👍）

链表基础

什么时候使用数组，什么时候考虑使用链表呢？

首先，链表是随机存储的，数组是连续存储的。

对于数组来说，在有随机访问需求时更适合使用。并且，由于只能一次性地申请一片内存空间，所以数组更适用于有固定大小数据的需求。

对于链表来说，在考虑连续访问的需求时更适合使用。并且，链表的长度是不固定的，可以申请新空间也可以删除旧数据，适合不确定数据量的需求。

• tips：在遇到链表问题时，maybe可以考虑一下快慢指针是否使用题目场景。

链表的定义

// 单链表
struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {} // 节点的构造函数
};
// 初始化节点
ListNode* head = new ListNode(5);

移除链表中的元素（203）

这一道题中所述的链表是一个不含头节点的链表，所以对其进行处理时需要进行分类讨论：

①如果处理的是头节点，那么需要找到第一个不等于val的值的节点，并且将这个节点赋为头节点；

②如果处理的是非头节点，那么只需将这个节点删除即可。

因此，处理这个问题时有两种方法，一种是按部就班对链表按照两种情况进行分类讨论，或者是创建一个虚拟头节点，将两种情归并为一种。

在处理这道算法题时遇到的语法问题：new ListNode(x)的定义、取值、赋值问题

// 初始化一个空节点，没有赋值，指针指向list
ListNode list = new ListNode();

// 初始化一个空节点，初始赋值为0，指针指向list
ListNode list = new ListNode(0);

// 初始化一个空节点，初始值赋为0，并且list的下一个指针指向head，指针指向list
ListNode list = new ListNode(0, head);

// 定义一个空链表
ListNode list = null;

设计链表（707）

对于这道题来说，问题不是出在如何对链表进行增删改查上，而是卡在语法上以及隐含的条件上。

隐含的条件：需要考虑用例链表是否为空？指针指向的节点是头节点？尾节点？空节点的情况。

翻转链表（206）

这种类型的题目在cs考研里属于是重点算法题目，所以我对其核心思想印象还是很深刻的（主要是双指针法这一个方法）。

在代码随想录中，还讲述了递归法的方法。对照着双指针的方法想，每一次传入的就是当前指向的节点以及其前一个节点，当当前指向节点为空指针时，递归结束。

两两交换链表中的节点（24）

这一题主要是对过程进行模拟，使用图的方式模拟流程很关键。

删除链表的倒数第N个节点（19）

在考虑使用一次循环解决这一个问题时，我的第一反应是使用递归的方法，但是尝试了一下没有写出来。求助于gpt后，核心代码如下：

int removeNthFromEndHelper(ListNode *node, int n) 
{
    if (!node) return 0;
    int index = removeNthFromEndHelper(node->next, n) + 1;
    if (index == n + 1) 
    {
        node->next= node->next->next;
    }
    return index;
}

我的错误思路是递归函数返回需要删除的节点，这样一来就没有办法计数了。在gpt大跌给出的方法中，直接使用一个递归函数完成了计数+删除节点的操作。

在阅读了题解的快慢指针后，感到恍然大悟，牛逼！快慢指针作为csky算法常考题没有立刻想起来，有点可惜。

链表香蕉（160）

这一道题的思想还是挺简单的，将两个链表对齐即可。

环形链表（142）

看了题解之后。。。这就是数学题吧）（有点像这种题目：两人相向而行 中间有一只狗跑来跑去 问两人相遇时 狗走了多远，小学噩梦，到现在还不会做。。。。）

这个题使用快慢指针的方法，具体可以分为两个步骤：①判断是否有环；②查找入环的第一个节点。

1. 令快指针每次移动两步，慢指针每次移动一步，如果链表有环，那么两个指针一定会在环里某一个位置相遇（追及问题）。

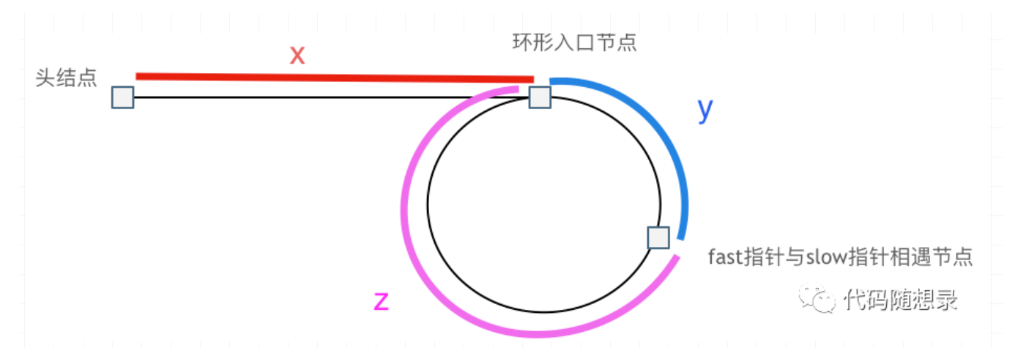
2. 如图所示，当fast和slow指针相遇时，fast已经走过的路程为：x + n (y + z) + y（假设在环中已经走了n圈）；slow已经走过的路程为：x + y。

   由于fast每次走两步，slow每次走一步，可以得到这样的等式：

   2 * (x + y) = x + n (y + z) + y

   整理可得：

   x = n * (y + z) - y => x = (n - 1)(y + z) + z。

   也就是说，假设环的总长度为L（L = y + z），x 和 z 之间存在相差 (n - 1)个L的关系，且 x > z。令两个指针分别从头节点和相遇节点出发，最终一定会在入口节点相遇。